
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值4,最小值1,设
上有最大值4,最小值1,设![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程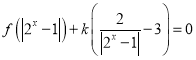 有四个不同的实数解,求实数
有四个不同的实数解,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】以下给出对程序框图的几种说法:
①任何一个程序框图都必须有起止框;②输入框只能紧接开始框,输出框只能紧接结束框;③判断框是唯一具有超出一个退出点的符号;④对于一个问题的算法来说,其程序框图判断框内的条件的表述方法是唯一的.
其中正确说法的个数是__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξ+η=8,若ξ~B(10,0.6),则E(η),D(η)分别是 ( )
A. 6和2.4 B. 2和2.4
C. 2和5.6 D. 6和5.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是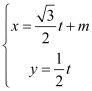 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
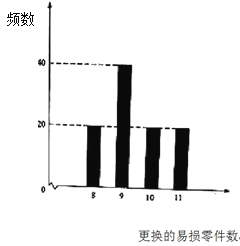
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(I)求![]() 的分布列;
的分布列;
(II)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(III)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是公理的是
A. 在空间中,如果两个角的两条边对应平行,那么这两个角相等或互补
B. 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
C. 平行于同一条直线的两条直线平行
D. 如果两个平行平面同时与第三个平面相交,那么它们的交线平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[m,n]上的奇函数,且f(x)在[m,n]上的最大值为a,则函数F(x)=f(x)+3在[m,n]上的最大值与最小值之和为( )
A.2a+3
B.2a+6
C.6-2a
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com