

科目:高中数学 来源: 题型:
| A、假设a,b,c不都是偶数 |
| B、假设a,b,c都不是偶数 |
| C、假设a,b,c至多有一个是偶数 |
| D、假设a,b,c至多有两个是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
4
| ||
| 3 |
A、[-
| ||||||||
B、(-
| ||||||||
C、[
| ||||||||
D、(-∞,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
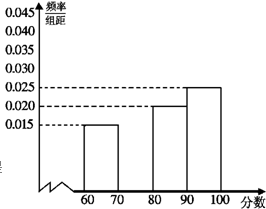 某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:
某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:| 考评得分 | [60,70) | [70,80) | [80,90) | [90,100) |
| 评定类型 | D | C | B | A |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax2-lnx+b |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |
| A、11元 | B、11.5元 |
| C、12元 | D、12.5元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com