
分析 (1)根据基本不等式即可求出函数的最小值,
(2)原不等式化为(x-2)(ax-1)≤0,再分类讨论即可求出不等式的解集.
解答 解:(1)a=1时,当x∈[1,+∞)时,函数$\frac{f(x)}{x}$=x+$\frac{2}{x}$-1≥2$\sqrt{x•\frac{2}{x}}$-1=2$\sqrt{2}$-1,当且仅当x=$\sqrt{2}$时取等号,
故函数$\frac{f(x)}{x}$的最小值为2$\sqrt{2}$-1,
(2)f(x)-2ax≤0,
即ax2-x+2-2ax≤0,
即(x-2)(ax-1)≤0,
当a=0时,解得x≥2,即解集为[2,+∞)
当a<0时,解得x≤$\frac{1}{a}$或x≤2,即解集为(-∞,$\frac{1}{a}$]∪[2,+∞)
当0<a<$\frac{1}{2}$时,解得2≤x≤$\frac{1}{a}$,即解集为[2,$\frac{1}{a}$]
当a=$\frac{1}{2}$时,解得x=2,即解集为{2}
当a>$\frac{1}{2}$时,解得得$\frac{1}{a}$≤x≤2,即解集为[$\frac{1}{a}$,2]
点评 本题考查了基本不等式的应用和含有参数的一元二次不等式的解法,属于中档题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
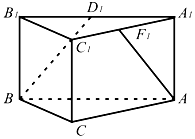 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | (0,4] | C. | [0,4) | D. | [0,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com