练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝x2－mx－mlnx．

    (1)设曲线y＝f(x)在点(1，f(1))处的切线与x轴平行．

    ①求f(x)的最值；

    ②若数列{an}满足a1＞e＋1(e为自然对数的底数)，an+1＝f(an)＋1，n∈N*，求证：．

    (2)设方程x＋lnx＝0的实根为x0．

    求证：对任意，存在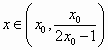使f(x)＞x2－ln(1＋ex)成立．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f(x)＝x2＋mx(m∈R)，则下列命题中的真命题是                        (　　)．

    A．任意m∈R，使y＝f(x)都是奇函数

    B．存在m∈R，使y＝f(x)是奇函数

    C．任意m∈R，使y＝f(x)都是偶函数

    D．存在m∈R，使y＝f(x)是偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)＝x2－1＋cosx(a>0)．

    (1)当a＝1时，证明：函数y＝f(x)在(0，＋∞)上是增函数；

    (2)若y＝f(x)在(0，＋∞)上是单调增函数，求正数a的范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年四川省高三10月月考理科数学试卷（解析版） 题型：选择题

     对实数a和b，定义运算“⊕”：a⊕b＝设函数f(x)＝(x2－2)⊕(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是

    A．(－∞，－2]∪            B．(－∞，－2]∪

    C. ∪              D. ∪

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年黑龙江省高三上学期期末考试数学理卷 题型：解答题

    、（12分）设函数f(x) ＝ x2＋bln(x＋1),

    （1）若对定义域的任意x，都有f(x)≥f(1)成立，求实数b的值；

    （2）若函数f(x)在定义域上是单调函数，求实数b的取值范围；

    （3）若b＝－1，证明对任意的正整数n，不等式成立；

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖南省十二校高三第一次联考数学文卷 题型：填空题

    设函数f(x)＝x2＋3，对任意x∈[1，＋∞)，f()＋m2f(x)≥f(x－1)＋3f(m)恒成立，则实数m的取值范围是　　　　　　　　　　　　　.


     

    查看答案和解析>>

    同步练习册答案