练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

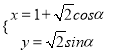    【题目】在直角坐标系中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρsin（θ+）= ，曲线C的参数方程为 （α为参数）．

    （1）求直线l的普通方程；

    （2）若P是曲线C上的动点，求点P到直线l的最大距离及点P的坐标．

    【答案】（1）x+y﹣5=0．（2）P（0，﹣1）．距离最大值 ．

    【解析】试题分析：（1）根据 将直线l的极坐标方程化为直角坐标方程（2）根据点到直线距离公式得三角函数关系式，再根据三角函数有界性确定最大值以及对应点P的坐标．

    试题解析：解：（1）直线l的极坐标方程为ρsin（θ+）=，

    展开可得：（sinθ+cosθ）=，

    可得x+y﹣5=0．

    （2）曲线C的参数方程为（α为参数）．可设P（1+cosα，sinα）．

    则点P到直线l的距离d==2﹣sin，

    当sin=﹣1时，d取得最大值3．

    取α=，可得P（0，﹣1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设G为△ABC的重心，过G作直线l分别交线段AB，AC（不与端点重合）于P，Q．若 =λ ， =μ
    （1）求 + 的值；
    （2）求λμ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制，发布成绩使用等级制．各等级划分标准如下：85分及以上，记为A等；分数在[70，85）内，记为B等；分数在[60，70）内，记为C等；60分以下，记为D等．同时认定A，B，C为合格，D为不合格．已知某学校学生的原始成绩均分布在[50，100]内，为了了解该校学生的成绩，抽取了50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出样本频率分布直方图如图所示．

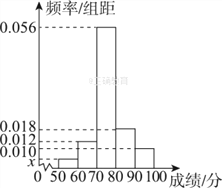
    （Ⅰ）求图中x的值，并根据样本数据估计该校学生学业水平测试的合格率；

    （Ⅱ）在选取的样本中，从70分以下的学生中随机抽取3名学生进行调研，用X表示所抽取的3名学生中成绩为D等级的人数，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

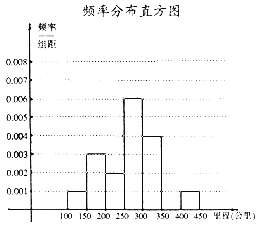
    【题目】面对全球范围内日益严峻的能源形势与环保压力，环保与低碳成为今后汽车发展的一大趋势，越来越多的消费者对新能源汽车表示出更多的关注，某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程（单次充电后能行驶的最大里程），被调查汽车的续航里程全部介于100公里和450公里之间，根据调查数据形成了如图所示频率分布表及频率分布直方图．

    频率分布表

    分组

    频数

    频率

    [100，150）

    1

    0.05

    [150，200）

    3

    0.15

    [200，250）

    x

    0.1

    [250，300）

    6

    0.3

    [300，350）

    4

    0.2

    [350，400）

    3

    y

    [400，450]

    1

    0.05

    合计

    N

    1

    （1）试确定频率分布表中x，y，N的值，并补全频率分布直方图；

    （2）若从续航里程在[200，250）及[350，400）的车辆中随机抽取2辆车，求两辆车续航里程都在[350，400）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中，且.

    （1）求值；

    （2）若，为自然对数的底数，求证：当时，；

    （3）若函数为上的单调函数，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的离心率为，且过点.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）已知椭圆的左焦点为，直线与椭圆交于不同两点，（都在轴上方），且.

    （ⅰ）若点的横坐标为1，求的面积；

    （ⅱ）直线是否恒过定点？若过定点，求出该定点的坐标；若不过定点，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某社区为丰富居民节日活动，组织了“迎新春”象棋大赛，已知由1,2,3号三位男性选手和4,5号两位女性选手组成混合组参赛.已知象棋大赛共有三轮，设三位男性选手在一至三轮胜出的概率依次是；两名女性选手在一至三轮胜出的概率依次是.

    （Ⅰ）若该组五名选手与另一组选手进行小组淘汰赛，每名选手只比赛一局，共五局比赛，求该组两名女性选手的比赛次序恰好不相邻的概率；

    （Ⅱ）若一位男性选手因身体不适退出比赛，剩余四人参加个人比赛，比赛结果相互不影响，设表示该组选手在四轮中胜出的人数，求随机变量的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场举行节日促销活动，消费满一定数额即可获得一次抽奖机会，抽奖这可以从以下两种方式中任选一种进行抽奖.

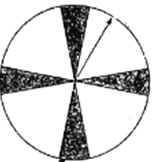
    抽奖方式①：让抽奖者随意转动如图所示的圆盘，圆盘停止后指针指向阴影部分（图中四个阴影部分均为扇形，且每个扇形圆心角均为，边界忽略不计）即中奖.

    抽奖方式②：让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球（球除颜色外不加区分），如果摸到的是2个红球，即中奖.

    假如你是抽奖者，为了让中奖的可能性大，你应该选择哪一种抽奖方式？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题：（1）函数f（x）在[0，+∞）上是增函数，在（﹣∞，0）上也是增函数，所以f（x）在R上是增函数；（2）若函数f（x）=ax2+bx+2与x轴没有交点，则b2﹣8a＜0，且a＞0； （3）y=x2﹣2|x|﹣3的递增区间为[1，+∞）；（4）函数y=lg10x和函数y=elnx表示相同函数．其中正确命题的个数是（ ）
    A.3
    B.2
    C.1
    D.0

    查看答案和解析>>

    同步练习册答案