
【题目】已知函数f(x)= ![]() .
.
(1)计算f(3),f(4),f( ![]() )及f(
)及f( ![]() )的值;
)的值;
(2)由(1)的结果猜想一个普遍的结论,并加以证明;
(3)求值f(1)+f(2)+…+f(2017)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ).
).
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( ) 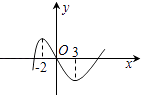
A.[0,3)
B.[﹣2,3]
C.(﹣∞,﹣2)
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査,右表是在某单位得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
附表:
P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
(1 )能否有90%以上的把握认为对这一问题的看法与性别有关?
【答案】解:解:K2= ![]() ≈2.932>2.706,
≈2.932>2.706,
由此可知,有90%的把握认为对这一问题的看法与性别有关
(1)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率; (ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
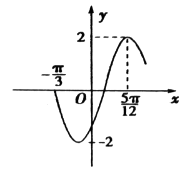
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或x> ![]() },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )
A.{x|x<﹣1或x>﹣lg2}
B.{x|﹣1<x<﹣lg2}
C.{x|x>﹣lg2}
D.{x|x<﹣lg2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com