
分析 由题意可得,x≥2时,(x+a)|x+a|+(ax)•x≤0恒成立,分类讨论,求得a的范围,可得a的最大值.
解答 解:对任意的x≥2,都有(x+a)|x+a|+(ax)|x|≤0,即 x≥2时,(x+a)|x+a|+(ax)•x≤0恒成立.
①若x+a≥0,即a≥-2时,则有(x+a)2+ax2≤0,∴(a+1)x2+2ax+a2≤0.
令f(x)=(a+1)x2+2ax+a2,则有a+1=0,或$\left\{\begin{array}{l}{a+1<0}\\{-\frac{2a}{2(a+1)}<2}\\{f(2)=4(a+1)+4a{+a}^{2}≤0}\end{array}\right.$,
求得a=-1,或-4-2$\sqrt{3}$≤a≤-4+2$\sqrt{3}$,综合可得-4-2$\sqrt{3}$≤a≤-2 或a=-1.
②若x+a<0,即a<-2时,则有-(x+a)2+ax2≤0,∴(a-1)x2-2ax-a2≤0.
令g(x)=(a-1)x2-2ax-a2,则它的图象的对称轴为x=$\frac{a}{a-1}$<0,g(2)=-4-a2≤0恒成立.
即此时,a的范围为 a<-2.
③若x+a=0,即a=-x≤-2 时,则由题意可得ax2≤0,满足条件.
综合①②③可得,a≤-2或-4-2$\sqrt{3}$≤a≤-2 或a=-1,故a的最大值为-1,
故答案为:-1.
点评 本题主要考查绝对值不等式的解法,分段函数的应用,二次函数的性质,属于难题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 18 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
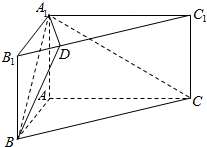 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,5] | B. | (0,5) | C. | [5,+∞) | D. | (5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com