解:(1)满足不等式组
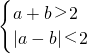
,
即满足
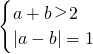
或
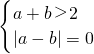
的有:(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5),(5,6),(6,5),(6,6)共15个.
所以a,b,c能构成三角形的概率为
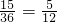
;
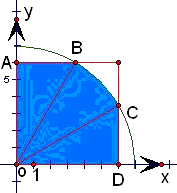
(2)(a,b)可以看成平面中的点.
试验的全部结果所构成的区域为U={(a,b)|0<a<6,0<b<6},
这是一个正方形区域,面积为S
U=6×6=36.
记“a,b,c能构成三角形”为事件A,
则构成事件A的区域A={(a,b)|0<a
2+b
2<48,0<a<6,0<b<6},
它表示的区域为图中阴影部分,其中OA=6,OB=4

,∴∠AOB=30,
同样,∠DOC=30°∴∠BOC=30°,
∴A的面积
=2S
△OAB+S
扇形OBC
=2×

+

=6×2

+
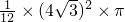
=12

+4π.
由几何概型,
所以P(A)=
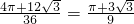
.
分析:(1)把(a,b)看成一个基本事件,则基本事件总数有36个,满足条件满足
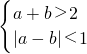
或
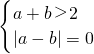
的基本事件有15个,这15个都能构成三角形,最后利用等可能事件的概率公式得到能构成三角形的概率.
(2)a,b,c能构成满足题意的直角三角形的充要条件是 0<a
2+b
2<48,0<a<6,0<b<6,在坐标系aob内画出满足以上条件的区域,如图所示,根据几何概型的计算方法即可求得结果.
点评:本题考查古典概型和几何概型的概率.几何概型估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
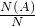
求解.属中档题.

 的直角三角形的概率.
的直角三角形的概率.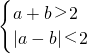 ,
,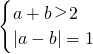 或
或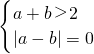 的有:(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5),(5,6),(6,5),(6,6)共15个.
的有:(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5),(5,6),(6,5),(6,6)共15个.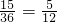 ;
; (2)(a,b)可以看成平面中的点.
(2)(a,b)可以看成平面中的点. ,∴∠AOB=30,
,∴∠AOB=30, +
+
 +
+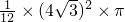
 +4π.
+4π.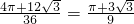 .
.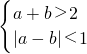 或
或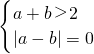 的基本事件有15个,这15个都能构成三角形,最后利用等可能事件的概率公式得到能构成三角形的概率.
的基本事件有15个,这15个都能构成三角形,最后利用等可能事件的概率公式得到能构成三角形的概率.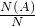 求解.属中档题.
求解.属中档题. 

 阅读快车系列答案
阅读快车系列答案