
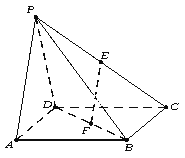
【题目】如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB. 
(I)求证:平面BCE⊥平面CDE;
(II)求平面BCE与平面ADEB所成锐二面角的余弦值.
【答案】(Ⅰ)证明:取CD的中点F,EC的中点P,连接BP,PF, 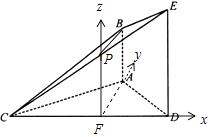
∴PF∥ED,PF= ![]() ,
,
由已知得,AB∥DE,AB= ![]() DE,
DE,
∴AB∥PF,AB=PF,则四边形ABPF为平行四边形,得BP∥AF,
∵AB∥DE,AB⊥平面ACD,∴DE⊥平面ACD,
又AF平面ACD,∴AF⊥ED.
又△ACD是等腰三角形,F是CD的中点,∴AF⊥CD.
∴BP⊥DE,BP⊥CD,又DE∩CD=D,∴BP⊥平面CDE.
又BP平面BCE,∴平面BCE⊥平面CDE;
(Ⅱ)解:以F为坐标原点,分别以FD、FA、FP所在直线为x、y、z轴建立空间直角坐标系,
设AD=2,∵∠CAD=120°,∴CD= ![]() ,
,
则C( ![]() ,0,0),D(
,0,0),D( ![]() ,0,0),A(0,1,0),B(0,1,1),E(
,0,0),A(0,1,0),B(0,1,1),E( ![]() ,0,2).
,0,2).
∴ ![]() ,
,
设平面BCE的一个法向量为 ![]() ,
,
则 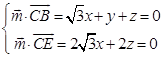 ,取x=1,得
,取x=1,得 ![]() .
.
又 ![]() ,
, ![]() .
.
设平面ADEB的一个法向量 ![]() ,
,
则 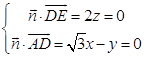 ,令x=1,得
,令x=1,得 ![]() .
.
设平面BCE与平面ADEB所成的锐角为θ,
则cosθ=|cos< ![]() >|=
>|= ![]() .
.
【解析】(Ⅰ)取CD的中点F,EC的中点P,连接BP,PF,由已知结合三角形中位线定理可得四边形ABPF为平行四边形,得BP∥AF,进一步求得DE⊥平面ACD,得到AF⊥ED.再由△ACD是等腰三角形,F是CD的中点,得到AF⊥CD.由线面垂直的判定可得BP⊥平面CDE.则平面BCE⊥平面CDE;(Ⅱ)以F为坐标原点,分别以FD、FA、FP所在直线为x、y、z轴建立空间直角坐标系,由已知求出所用点的坐标,得到平面BCE与平面ADEB的一个法向量,由两法向量所成角的余弦值可得平面BCE与平面ADEB所成锐二面角的余弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】如图,圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦.
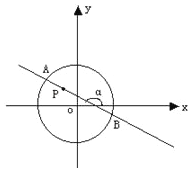
(1)当弦AB被点P平分时,求直线AB的方程;
(2)求过点P的弦的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|xex|,又g(x)=[f(x)]2﹣tf(x)(t∈R),若方程g(x)=﹣2有4个不同的根,则t的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的方程为
的方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)当![]() 时,判断直线
时,判断直线![]() 与圆
与圆![]() 的关系;
的关系;
(2)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标![]() 系中,直线
系中,直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)①当![]() 时,写出直线
时,写出直线![]() 的普通方程;
的普通方程;
②写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=x2+5,记a=f(﹣log25),b=f(log23),c=f(﹣1),则a,b,c的大小关系为( )
A.c<b<a
B.a<c<b
C.c<a<b
D.a<b<c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com