
【题目】为了实现绿色发展,避免能源浪费,某市计划对居民用电实行阶梯收费.阶梯电价原则上以住宅(一套住宅为一户)的月用电量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯电量 | 第二阶梯电量 | 第三阶梯电量 |
月用电量范围(单位: |
|
|
|
从本市随机抽取了100户,统计了今年6月份的用电量,这100户中用电量为第一阶梯的有20户,第二阶梯的有60户,第三阶梯的有20户.
(1)现从这100户中任意选取2户,求至少1户用电量为第二阶梯的概率;
(2)以这100户作为样本估计全市居民的用电情况,从全市随机抽取3户,![]() 表示用电量为第二阶梯的户数,求
表示用电量为第二阶梯的户数,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() (如图②).在折起的过程中,下列说法中错误的个数是( )
(如图②).在折起的过程中,下列说法中错误的个数是( )
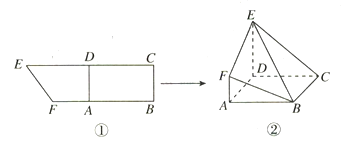
①![]() 平面
平面![]() ;
;
②![]() 四点不可能共面;
四点不可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.
可能垂直.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人做定点投篮游戏,已知甲每次投篮命中的概率均为![]() ,乙每次投篮命中的概率均为
,乙每次投篮命中的概率均为![]() ,甲投篮3次均未命中的概率为
,甲投篮3次均未命中的概率为![]() ,甲、乙每次投篮是否命中相互之间没有影响.
,甲、乙每次投篮是否命中相互之间没有影响.
(1)若甲投篮3次,求至少命中2次的概率;
(2)若甲、乙各投篮2次,设两人命中的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 2013湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: 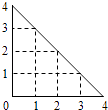
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰 好“相近”的概率;
(2)在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 ![]() 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com