
【题目】在极坐标系下,已知直线 ![]() (
( ![]() )和圆
)和圆 ![]() .圆
.圆 ![]() 与直线
与直线 ![]() 的交点为
的交点为 ![]() .
.
(1)求圆 ![]() 的直角坐标方程,并写出圆
的直角坐标方程,并写出圆 ![]() 的圆心与半径.
的圆心与半径.
(2)求 ![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】为了丰富改善居民生活,市招商局引进外商到开发区一次性投资72万元建起了一座蔬菜加工厂.以后每年还需要继续投资:第一年需要要各种经费为12万元,从第二年开始每年所需经费均比上一年增加4万元,该加工厂每年销售总收入为50万元.
(1)若扣除投资及各种经费,该加工厂从第几年开始纯利润为正?
(2)若干年后,外商为开发新项目,对加工厂有两种处理方案:
①若年平均纯利润达到最大值时,便以48万元价格出售该厂;
②若纯利润总和达到最大值时,便以16万元的价格出售该厂.
问:哪一种方案比较合算?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)已知集合X={1,2,3},Yn={1,2,3...,n}(n![]() N*),Sn={(a,b)|a整除b或b整除a, a
N*),Sn={(a,b)|a整除b或b整除a, a![]() X, b
X, b![]() Yn}, 令f(n)表示集合Sn所包含元素的个数。
Yn}, 令f(n)表示集合Sn所包含元素的个数。
(1)写出f(6)的值;
(2)当n≥6时,写出f(n)的表达式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
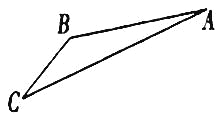
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】F1、F2为椭圆的两个焦点,以F2为圆心作圆F2 , 已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为( )
A.![]() ﹣1
﹣1
B.2﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
查看答案和解析>>
科目:高中数学 来源: 题型:
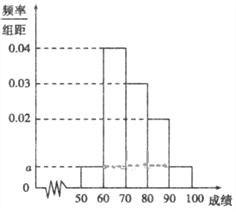
【题目】某校![]() 名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:
名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1).求图中![]() 的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2).若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如上右表所示,求数学成绩在
)之比如上右表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com