
����Ŀ��ij��ѧ��ʦ�Ա�У2013�����ѧ��ij����������ѧ�ɼ����з�������1��50���зֲ������ȡ20��ѧ���ijɼ����з����������þ�Ҷͼ��¼��ͼ��ʾ���������ݶ�ʧ�����õ���Ƶ�ʷֲ������£� 
�����Σ��֣� | [50��70] | [70��90] | [90��110] | [110��130] | [130��150] | �ϼ� |
Ƶ�� | b | |||||
Ƶ�� | a | 0.25 |
��1������a��b��ֵ��������[90��100����Χ�ڵ�ѧ������������ο���ȫУѧ����ѧ�ɼ������ʣ�������[90��150]��ΧΪ����
��2���Ӵ��ڵ���110�ֵ�ѧ�����ѡ2��ѧ���÷֣���2��ѧ����ƽ���÷ִ��ڵ���130�ֵĸ��ʣ�
���𰸡�
��1���⣺�ɾ�Ҷͼ��֪������[50��70����Χ�ڵ���2�ˣ���[110��130����Χ�ڵ���3�ˣ�
��a= ![]() ��b=3��
��b=3��
�ַ�����[110��150����Χ�ڵ�Ƶ��Ϊ ![]() ��
��
�������[90��110����Χ�ڵ�Ƶ��Ϊ1��0.1��0.25��0.25=0.4��
�������[90��110����Χ�ڵ�����Ϊ20��0.4=8��
�ɾ�Ҷͼ��֪����[100��110����Χ�ڵ�����Ϊ4�ˣ�
�������[90��100����Χ�ڵ�ѧ����Ϊ8��4=4���ˣ���
�Ӿ�Ҷͼ��֪������[70��90]��Χ�ڵ�Ƶ��Ϊ0.3��������20��0.3=6���ˣ���
����ѧ�ɼ������ѧ��Ϊ13�ˣ�
�����ȫУ��ѧ�ɼ�������Ϊ ![]() %��
%��
��2���⣺��A��ʾ�¼������ڵ���100�ֵ�ѧ�������ѡ2��ѧ���÷֣�ƽ���÷ִ��ڵ���130�֡���
�ɾ�Ҷͼ��֪���ڵ���100����5�ˣ�����5�˷ֱ�Ϊa��b��c��d��e��
��ѡȡѧ�������п��ܽ��Ϊ����a��b������a��c������a��d������a��e������b��c������b��d������b��e������c��d������c��e������d��e���������¼���Ϊ10��
�¼���2��ѧ����ƽ���÷ִ��ڵ���130�֡�Ҳ���ǡ�������ѧ���ķ���֮�ʹ��ڵ���260����
���Կ��ܽ��Ϊ����118��142������128��136������128��142������136��142����
��4������������¼���Ϊ4��
�� ![]() ��
��
����������1�����ݾ�Ҷͼ�������a��b��ֵ����������ο���ȫУѧ����ѧ�ɼ������ʣ�������[90��150]��ΧΪ������2�������б�������Ϲŵ������2��ѧ����ƽ���÷ִ��ڵ���130�ֵĸ��ʣ�
�����㾫����������Ҫ������Ƶ�ʷֲ����;�Ҷͼ�����֪ʶ�㣬��Ҫ���յ�һ������ڶ����������������������������ȷ���ֵ㣬�����ݷ��飻���IJ�����Ƶ�ʷֲ�������Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��ٲ�����ȷ�����⣮


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �������
�������![]() �ķ���
�ķ���![]() ��
��![]() ����ͬ��ʵ���⣬��
����ͬ��ʵ���⣬��![]() �����п��ܵ�ֵΪ�� ��
�����п��ܵ�ֵΪ�� ��
A. 3 B. 1��3 C. 4��6 D. 3��4��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cos2 ![]() ��sin
��sin ![]() cos
cos ![]() ��
�� ![]() ��
��
��1������f��x������С�����ں�ֵ��
��2���� ![]() ����sin2����ֵ��
����sin2����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�����ȷ����
����ij������У��������![]() ������̬�ֲ�
������̬�ֲ�![]() .��
.��![]() ��
��![]() ��ȡֵ�ĸ���Ϊ0.35����
��ȡֵ�ĸ���Ϊ0.35����![]() ��
��![]() ��ȡֵ�ĸ���Ϊ0.7��
��ȡֵ�ĸ���Ϊ0.7��
����ģ��![]() ȥ���һ������ʱ��Ϊ������ع鷽�̣���
ȥ���һ������ʱ��Ϊ������ع鷽�̣���![]() ����任��õ����Իع鷽��
����任��õ����Իع鷽��![]() ����
����![]() ��
��
����֪������������![]() ��
��![]() ��������������
��������������![]() �����������������
�����������������![]() ������
������![]() ��
��![]() ���Ǽ��������������⣻
���Ǽ��������������⣻
���賣��![]() ����ʽ
����ʽ![]() ��
��![]() ������ij�Ҫ������
������ij�Ҫ������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǻ���![]() ��ͼ�����������⣺
��ͼ�����������⣺
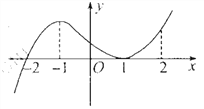
��![]() �Ǻ���
�Ǻ���![]() �ļ�ֵ��
�ļ�ֵ��
��1�Ǻ���![]() �ļ�Сֵ��
�ļ�Сֵ��
��![]() ��
��![]() �����ߵ�б�ʴ�����
�����ߵ�б�ʴ�����
��![]() ������
������![]() �ϵ����ݼ�
�ϵ����ݼ�
����ȷ����������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() [
[ ![]() sin��x��
sin��x�� ![]() ��]��
��]��
��1����f��x���Ķ������ֵ��
��2��˵��f��x������ż�ԣ�
��3����f��x���ĵ��������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�õ�����y=2cosxsin��x+ ![]() ����
���� ![]() ��ͼ��ֻ�轫y=sinx��ͼ�� ��
��ͼ��ֻ�轫y=sinx��ͼ�� ��
A.������ƽ�� ![]() ����λ���ȣ��ٽ����е�ĺ���������Ϊԭ����
����λ���ȣ��ٽ����е�ĺ���������Ϊԭ���� ![]() ���������겻�䣩
���������겻�䣩
B.������ƽ�� ![]() ����λ���ȣ��ٽ����е�ĺ���������Ϊԭ����2���������겻�䣩
����λ���ȣ��ٽ����е�ĺ���������Ϊԭ����2���������겻�䣩
C.�Ƚ����е�ĺ���������Ϊԭ����2���������겻�䣩��������ƽ�� ![]() ����λ����
�������
D.�Ƚ����е�ĺ���������Ϊԭ���� ![]() ���������겻�䣩��������ƽ��
���������겻�䣩��������ƽ�� ![]() ����λ����
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����������Σ���
�������������![]() ��ABCD��
��ABCD��
![]() ��
Ϊ��![]() ���е㣬MΪ�߶�
���е㣬MΪ�߶�![]() ���е�.
���е�.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �����.
�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����ⳤΪ2��������ABCD��A1B1C1D1�У�E��F�ֱ�ΪDD1��DB���е㣮 
��1����֤��EF��B1C��
��2��������E��FCB1�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com