Question

已知定义在上的奇函数满足，且在区间上是增函数，则当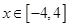时，不等式的解集为（    ）

A．

B．

C．

D．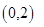

Answer 1

A

解析试题分析：：∵定义在R上的奇函数满足，
令x=x－4代入得f(x－8)=－f(x－4)=f(x)，
令x=x+8)代入上式得f(x)=f(x+8)，
∴函数f(x)为最小正周期是8的周期函数，
∵在区间[0，2]上是增函数，∴在区间[－2，0]上是增函数，在区间[－4，－2]上是减函数，
在区间[2，4]上是减函数，
即在区间[－4,4]上是函数f(x)的一个周期的图象，
∵xf‘（x）＜0，即x与f'(x)符号相反，
∴xf‘（x）＜0的解集为（－2，0）或（2，4），故选A。
考点：函数的奇偶性、单调性、周期性，应用导数研究函数的单调性。
点评：中档题，此类问题十分典型，利用数形结合思想，认识函数的性质，进一步确定不等式的解集。