
【题目】在贵阳市创建全国文明城市工作验收时,国家文明委有关部门对我校高二年级6名学生进行了问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.如果用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为( )
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .
.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(Ⅱ)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系为__________.(用“>”连接)
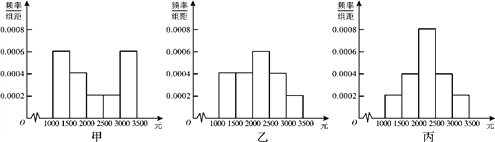
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全运会将于2017年9月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎、个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩的中位数 ;
(Ⅱ)从本次成绩在85分以上(含85分)的学员中任选2人,2人成绩都在90分以上(含90分)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC,已知PA⊥面ABC,AD⊥BC于D,BC=CD=AD=1,设PD=x,∠BPC=θ,记函数f(x)=tanθ,则下列表述正确的是( ) 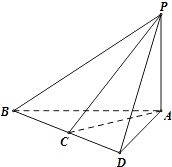
A.f(x)是关于x的增函数
B.f(x)是关于x的减函数
C.f(x)关于x先递增后递减
D.关于x先递减后递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com