
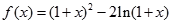 。
。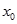 ,使不等式
,使不等式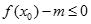 能成立,求实数
能成立,求实数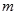 的最小值;
的最小值;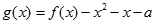 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。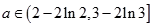
 能成立,求m最小值。可以转化成求函数
能成立,求m最小值。可以转化成求函数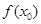 在定义域内的最小值。(2)函数
在定义域内的最小值。(2)函数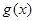 在
在 上有两个不同零点,所以
上有两个不同零点,所以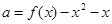 在
在 上有两个不同的解,可以令
上有两个不同的解,可以令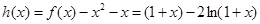 ,结合图形研究函数
,结合图形研究函数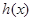 的性质即可。
的性质即可。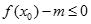 能成立,只需
能成立,只需 。 ………………1分
。 ………………1分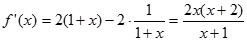 ,…………………………………2分
,…………………………………2分 的定义域为
的定义域为 , ……………………………………3分
, ……………………………………3分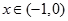 时,
时, ,∴函数
,∴函数 在区间
在区间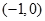 上是减函数;
上是减函数;  时,
时,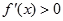 ,∴函数
,∴函数 在区间(0,+∞)上是增函数。 …………5分
在区间(0,+∞)上是增函数。 …………5分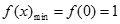 , ∴
, ∴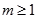 。故实数
。故实数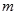 的最小值为1。……………………6分(Ⅱ)由
的最小值为1。……………………6分(Ⅱ)由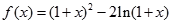 得:
得: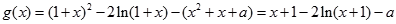 …………………7分
…………………7分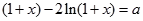 在区间
在区间 上恰有两个相异实根。
上恰有两个相异实根。 。∵
。∵ ,列表如下:
,列表如下: |  | 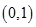 | | 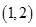 |  |
 | | - | 0 | + | |
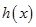 | | 减函数 |  | 增函数 | 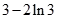 |
 ,∴
,∴ 。
。 ,
,
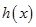 在区间
在区间 上的草图(见图),
上的草图(见图),
 在区间
在区间 上恰有两个相异实根,
上恰有两个相异实根,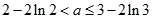 ,即:
,即: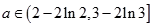 。 ……………12分
。 ……………12分

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
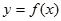 ,若同时满足下列条件:①
,若同时满足下列条件:①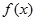 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[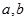 ]
]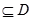 ,使
,使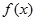 在[
在[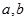 ]上的值域为[
]上的值域为[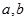 ];那么把
];那么把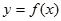 (
( )叫闭函数.
)叫闭函数.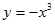 符合条件②的区间[
符合条件②的区间[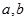 ];
];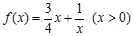 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;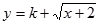 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com