
����Ŀ��ijˮ����ֳ���������ʱ������������в���100β�㣬�������ֱ���[4��4.5����[4.5.5����[5.5.5����[5.5��6����[6��6.5����[6.5��7]����λ����У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ
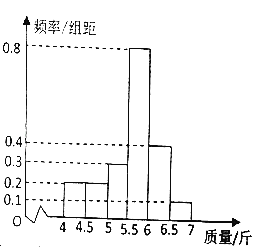
��1���ְ��ֲ�����ķ�����������Ϊ[4.5��5����[5��5.5�������������ȡ5β���ٴ���5β�������ȡ2β�����������X��ʾ������[4.5��5���ڵ����β������X�ķֲ��м���ѧ������
��2���Ը������ݵ��м��������������ݵ�ƽ��ֵ����Ƶ����Ϊ���ʣ�����ֳ����δ���̵����Լ����1000β����������������
����һ������ʣ�����������������������5.5������ۼ�Ϊÿ��10Ԫ����������5.5������ۼ�Ϊÿ��12Ԫ
��������һ�ܺ�����ʣ�������������������ÿβ����������䣬�����Ŀ���䣬��������5.5������ۼ�Ϊÿ��15Ԫ����������ֳһ�ܵķ�����ƽ��ÿβ22Ԫ����������5.5������ۼ�Ϊÿ��16Ԫ����������ֳһ�ܵķ�����ƽ��ÿβ24Ԫͨ������ȷ��ˮ����ֳ��ѡ�����ַ����������ࣿ
���𰸡���1����������![]() ����2��ˮ����ֳ��ѡ��һ�������࣮
����2��ˮ����ֳ��ѡ��һ�������࣮
��������
��1�������������β�������ݳ����ͷֲ�������ʣ��ó�X�ķֲ��к���ѧ������
��2���ֱ����������������β�����������ַ�����Ӧ���ۼ۵ó����ۣ�
��1��������[4.5��5����[5��5.5������β����Ϊ0.2��0.3����2��3��
�ʰ��ֲ�����ķ�����������Ϊ[4.5��5����[5��5.5�������������ȡ5β��
������[4.5��5��������2�������[5��5.5��������3�
��X�Ŀ���ȡֵΪ0��1��2��
P��X��0��![]() ��P��X��1��
��P��X��1��![]() ��P��X��2��
��P��X��2��![]() ��
��
X�ķֲ���Ϊ��
X | 0 | 1 | 2 |
P |
|
|
|
EX��0![]() 1
1![]() 2
2![]() ��
��
��2���ʰ���������һ��
��������������
4.25��10��1000��0.2��0.5+4.75��10��1000��0.2��0.5+5.25��10��1000��0.3��0.5+5.75��12��1000��0.8��0.5+6.25��12��1000��0.4��0.5+6.75��12��1000��0.1��0.5
��4250+4750+7875+27600+15000+4050
��63525��Ԫ����
��������������������������
4.25��15��1000��0.2��0.5+4.75��15��1000��0.2��0.5+5.25��15��1000��0.3��0.5+5.75��16��1000��0.8��0.5+6.25��16��1000��0.4��0.5+6.75��16��1000��0.1��0.5��24��1000
��6370+7125+11812.5+36800+20000+5400��24000
��63507��Ԫ����
��63525��63507��
��ˮ����ֳ��ѡ��һ�������࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1��Ϊijʡ2016����ҵ����ͳ�Ʊ���ͼ��2��ijʡ2016����ҵ������ͳ�Ʊ�����ͳ��ͼ�������������ǣ���
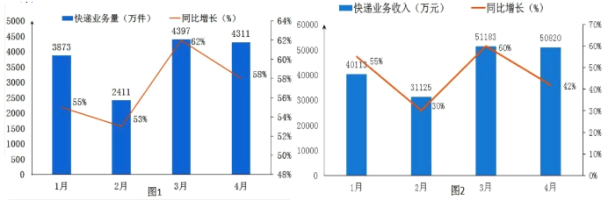
A.2016��1��4��ҵ�������3�����2�£���ֵ�ӽ�2000���
B.2016��1��4��ҵ����ͬ�������ʾ�����50������3����ߣ��ʹ����ݷ�������ӭ�������й�
C.����ͼ�п��������������ٶȲ�����ȫһ�£���ҵ������ҵ�������仯�߶�һ��
D.��1��4��������ҵ������ҵ���������в����������屣�ָ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��E��F�ֱ�ΪAB��CD���е㣬����ADE��DE����ʹ��ACDΪ�ȱ������Σ���ͼ��ʾ���Ƕ����A-DE-C�Ĵ�СΪ![]() .
.
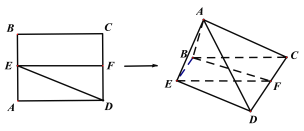
��1��֤������A��ƽ��BCDE�ڵ���ӰG��ֱ��EF�ϣ�
��2�����![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��![]() ��g��x����3elnx+mx��ͼ����4����ͬ�Ľ��㣬��ʵ��m��ȡֵ��Χ�ǣ� ��
��g��x����3elnx+mx��ͼ����4����ͬ�Ľ��㣬��ʵ��m��ȡֵ��Χ�ǣ� ��
A.����3��![]() ��B.����1��
��B.����1��![]() ��C.����1��3��D.��0��3��
��C.����1��3��D.��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧԺ2018����ɽ�����������������ܶ�.������Ա��ij��������ȡ�˸���2018�������������Գɼ���200��ѧ����ɫ�ʺ�����ij��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�������ͼ��ʾ.
��� | ���� | Ƶ�� | Ƶ�� |
��1�� |
| 24 | 0.12 |
��2�� |
| �� | 0.18 |
��3�� |
| 64 | 0.32 |
��4�� |
| 60 | �� |
��5�� |
| 16 | 0.08 |
�ϼ� | 200 | 1.00 | |
��1���������Ƶ�ʷֲ����Т١���λ����Ӧ���ݣ����ڴ���ֽ���������Ƶ�ʷֲ�ֱ��ͼ������Ƶ�ʷֲ�ֱ��ͼ������λ����
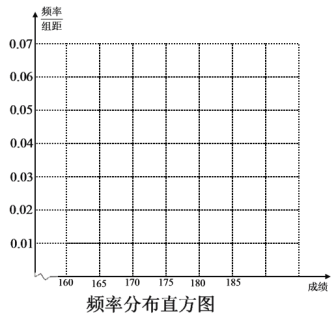
��2��Ϊ���ܸ�������˽����ѧ�������������Ժ�����ڸ�����ǰ�Ƚ��г�������.���ܳ��غͽ��������Ŀ����ƣ������ӵ�3��ѡ��3�ˣ���4��ѡ��2�ˣ���5��ѡ��1�ˣ�Ȼ�����6������ѡ��2�˽��е��У�����2�˾����Ե�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����xlnx+2x��1��
��1����f��x���ļ�ֵ��
��2�����������x��1������f��x����k��x��1����0��k��Z�����������k�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �����ҽ���
�����ҽ���![]() ��
��![]() ʱȡ����ֵ���Ҽ���ֵ�ȼ�Сֵ��
ʱȡ����ֵ���Ҽ���ֵ�ȼ�Сֵ��![]()
(1)��![]() ��
��![]() ֵ��
ֵ��
(2)���![]() �ļ���ֵ�ͼ�Сֵ.
�ļ���ֵ�ͼ�Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2������������a��ʹ��![]() ʱ��
ʱ��![]() ����ʵ��k��ȡֵ��Χ.
����ʵ��k��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com