
| A. | 27 | B. | 3 | C. | 27或3 | D. | 9 |
分析 求得双曲线的a,c,运用离心率公式可得b=8,c=10,运用双曲线的定义,可得|PF2|=27或3,讨论P在左支和右支上,结合双曲线的图象即可得到所求距离.
解答 解:双曲线$\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的a=6,c=$\sqrt{36+{b}^{2}}$,
由e=$\frac{c}{a}$=$\frac{\sqrt{36+{b}^{2}}}{6}$=$\frac{5}{3}$,
解得b=8,c=10.
由双曲线的定义可得2a=||PF1|-|PF2||,
即有12=|15-|PF2||,
解得|PF2|=27或3,
若P在左支上,可得|PF1|≥c-a=4,|PF2|≥a+c=16;
若P在右支上,可得|PF1|≥c+a=16>15,不成立.
综上可得,|PF2|=27.
故选:A.
点评 本题考查双曲线的定义、方程和性质,主要是离心率的运用,考查运算能力,属于基础题和易错题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{8}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | ($\frac{π}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-∞,2]∪[3,+∞) | C. | [-1,6] | D. | [-6,1] |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆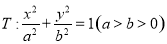 的离心率为
的离心率为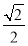 ,过左焦点
,过左焦点 的直线与椭圆交于
的直线与椭圆交于 两点,若线段
两点,若线段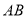 的中点为
的中点为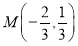 .
.
(1)求椭圆的方程;
(2)过右焦点的直线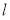 与圆
与圆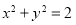 相交于
相交于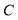 、
、 ,与椭圆
,与椭圆 相交于
相交于 、
、 ,且
,且 ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
已知a,b,c∈R,命题“若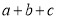 =3,则
=3,则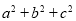 ≥3”的否命题是( )
≥3”的否命题是( )
A.若a+b+c≠3,则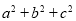 <3
<3
B.若a+b+c=3,则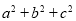 <3
<3
C.若a+b+c≠3,则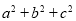 ≥3
≥3
D.若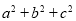 ≥3,则a+b+c=3
≥3,则a+b+c=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com