
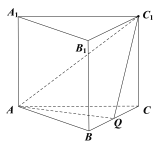
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面AQC1的距离.
到平面AQC1的距离.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,动点M到两定点A(﹣1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C. 
(1)求轨迹C的方程;
(2)设直线y=﹣2x+m与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图 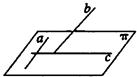
(1)证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )
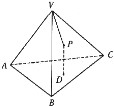
A. 直线 B. 抛物线
C. 离心率为![]() 的椭圆 D. 离心率为3的双曲线
的椭圆 D. 离心率为3的双曲线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时, ![]() 的坐标为 .
的坐标为 . 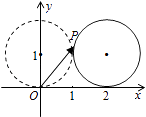
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF. 
(1)求证:BD⊥平面AED;
(2)求二面角F﹣BD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国人均读书![]() 本(包括网络文学和教科书),比韩国的
本(包括网络文学和教科书),比韩国的![]() 本、法国的
本、法国的![]() 本、日本的
本、日本的![]() 本、犹太人的
本、犹太人的![]() 本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成
名读书者进行调查,将他们的年龄分成![]() 段:
段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:

(1)估计在这![]() 名读书者中年龄分布在
名读书者中年龄分布在![]() 的人数;
的人数;
(2)求这![]() 名读书者年龄的平均数和中位数;
名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取
的读书者中任取![]() 名,求这两名读书者年龄在
名,求这两名读书者年龄在![]() 的人数恰为
的人数恰为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若函数f(x)=ax2-x-1有且仅有一个零点, 求实数a的值.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会会议提出“决胜全面建成小康社会”.某地随着经济的发展,居民收入逐年增长,下表是该地一银行连续五年的储蓄存款(年底余额),如表1:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 |
储蓄存款 | 5 | 6 | 7 | 9 | 12 |
为了计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() 得到下表2:
得到下表2:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 4 | 7 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到2035年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com