
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
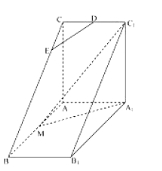
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记二次函数
中,记二次函数![]() (
(![]() )与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为
)与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设P为圆![]() 上一点,若直线PA,PB分别交直线
上一点,若直线PA,PB分别交直线![]() 于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论.
于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,乒乓球是中国的国球,乒乓球队内部也有着很严格的竞争机制,为了参加国际大赛,种子选手甲与三位非种子选手乙、丙、丁分别进行一场内部对抗赛,按以往多次比赛的统计,甲获胜的概率分别为![]() ,
,![]() ,
,![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若甲至少获胜两场的概率大于![]() ,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
(2)求甲获胜场次![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组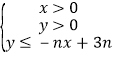 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
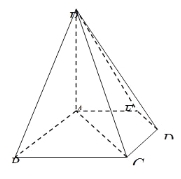
【题目】如图,在五棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 是等腰三角形.
是等腰三角形.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,若存在,求出
,若存在,求出![]() 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水![]() (单位:千克) 清洗该蔬菜
(单位:千克) 清洗该蔬菜![]() 千克后, 蔬菜上残留的农药
千克后, 蔬菜上残留的农药![]() (单位:微克) 的统计表:
(单位:微克) 的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在下面的坐标系中, 描出散点图, 并判断变量![]() 与
与![]() 的相关性;
的相关性;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程, 令
的回归方程, 令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中) ,求出
,完成以下表格(填在答题卡中) ,求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 精确到
精确到![]() )
)

|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害, 为了放心食用该蔬菜, 请
微克时对人体无害, 为了放心食用该蔬菜, 请
估计需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )
)
(附:线性回归方程![]() 中系数计算公式分别为;
中系数计算公式分别为;
 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com