Question

某电子科技公司开发一种新产品，公司对经营的盈亏情况每月最后一天结算1次．在1～12月份中，公司前x个月累计获得的总利润y（万元）与销售时间x（月）之间满足二次函数关系式y=a（x﹣h）2+k，二次函数y=a（x﹣h）2+k的一部分图象如图所示，点A为抛物线的顶点，且点A、B、C的横坐标分别为4、10、12，点A、B的纵坐标分别为﹣16、20．

（1）试确定函数关系式y=a（x﹣h）2+k；

（2）分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润；

（3）在前12个月中，哪个月该公司一个月内所获得的利润最多？最多利润是多少万元？

Answer 1

 

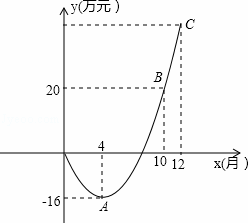
解答： 解：（1）根据题意可设：y=a（x﹣4）2﹣16，

当x=10时，y=20，

所以a（10﹣4）2﹣16=20，解得a=1，

所求函数关系式为：y=（x﹣4）2﹣16．﹣﹣﹣﹣﹣﹣﹣（4分）

（2）当x=9时，y=（9﹣4）2﹣16=9，所以前9个月公司累计获得的利润为9万元，

又由题意可知，当x=10时，y=20，而20﹣9=11，

所以10月份一个月内所获得的利润11万元．﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）

（3）设在前12个月中，第n个月该公司一个月内所获得的利润为s（万元）

则有：s=（n﹣4）2﹣16﹣[（n﹣1﹣4）2﹣16]=2n﹣9，

因为s是关于n的一次函数，且2＞0，s随着n的增大而增大，

而n的最大值为12，所以当n=12时，s=15，

所以第12月份该公司一个月内所获得的利润最多，最多利润是15万元．﹣﹣（4分）