
.给出下列命题,其中正确的两个命题是( )
①直线上有两点到平面的距离相等,则此直线与平面平行 ②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m⊥平面α,直线n⊥m,则n∥α ④a、b是异面直线,则存在唯一的平面α,使它与a、b都平行且与a、b距离相等
| A.①② | B.②③ | C.③④ | D.②④ |
D
解析考点:异面直线的判定;直线与平面平行的判定;平面与平面平行的判定.
分析:通过举反例可得①错误.利用面面平行的性质定理与线面平行的判定定理可确定②正确.③错误.直线n可能在平面α内.
④正确.设AB是异面直线a、b的公垂线段,E为AB的中点,过E作a′∥a,b′∥b,则a′、b′确定的平面即为与a、b都平行且与a、b距离相等的平面,并且它是唯一确定的. 解:①错误.如果这两点在该平面的异侧,则直线与平面相交.
解:①错误.如果这两点在该平面的异侧,则直线与平面相交.
②正确.如图,平面α∥β,A∈α,C∈α,D∈β,B∈β且E、F分别为AB、CD的中点,
过C作CG∥AB交平面β于G,连接BG、GD.
设H是CG的中点,则EH∥BG,HF∥GD.
∴EH∥平面β,HF∥平面β.
∴平面EHF∥平面β∥平面α.
∴EF∥α,EF∥β.
③错误.直线n可能在平面α内.
④正确.如图,设AB是异面直线a、b的公垂线段,E为AB的中点,过E作a′∥a,b′∥b,则a′、b′确定的平面即为与a、b都平行且与a、b距离相等的平面,并且它是唯一确定的.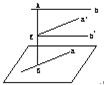


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:高中数学 来源: 题型:
 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有查看答案和解析>>
科目:高中数学 来源: 题型:
| a+m |
| b+m |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com