
【题目】如图,圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,与
,与![]() 正半轴交于点
正半轴交于点![]() ,与直线
,与直线![]() 在第一象限的交点为
在第一象限的交点为![]() .点
.点![]() 为圆
为圆![]() 上任一点,且满足
上任一点,且满足![]() ,以
,以![]() 为坐标的动点
为坐标的动点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.

(1)求圆![]() 的方程及曲线
的方程及曲线![]() 的方程;
的方程;
(2)若两条直线![]() 和
和![]() 分别交曲线
分别交曲线![]() 于点
于点![]() 和
和![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时的
面积的最大值,并求此时的![]() 的值.
的值.
(3)根据曲线![]() 的方程,研究曲线
的方程,研究曲线![]() 的对称性,并证明曲线
的对称性,并证明曲线![]() 为椭圆.
为椭圆.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 时,四边形
时,四边形![]() 的面积最大值为
的面积最大值为![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)由圆半径为圆心到切线距离得圆半径,从而得圆方程,由![]() 表示出
表示出![]() 点坐标代入圆
点坐标代入圆![]() 方程可得曲线
方程可得曲线![]() 的方程.
的方程.
(2)把![]() 方程代入曲线
方程代入曲线![]() 的方程求得
的方程求得![]() 的坐标,得
的坐标,得![]() ,同理可得
,同理可得![]() ,由
,由![]() 得
得![]() ,应用整体换元法结合基本不等式可求得最值(也可变形为
,应用整体换元法结合基本不等式可求得最值(也可变形为![]() ,求最值);
,求最值);
(3)由曲线![]() 的方程可得对称性:关于直线
的方程可得对称性:关于直线![]() 对称,关于原点对称,这个方程除右边是常数1外,左边是二次式且为和的形式,与我们所学椭圆的方程类似,因此可假设其为椭圆,再根据椭圆的性质求顶点坐标和焦点坐标,根据椭圆定义证明.
对称,关于原点对称,这个方程除右边是常数1外,左边是二次式且为和的形式,与我们所学椭圆的方程类似,因此可假设其为椭圆,再根据椭圆的性质求顶点坐标和焦点坐标,根据椭圆定义证明.
解:(1)由题意圆![]() 的半径
的半径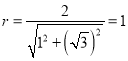 ,
,
故圆![]() 的方程为
的方程为![]() .
.
由![]() 得,
得,![]() ,将
,将![]() 代入
代入![]()
得![]() 为曲线
为曲线![]() 的方程.
的方程.
(2)由![]()
得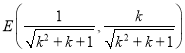 ,
, ,
,
所以![]() ,同理
,同理 .
.
由题意知![]() ,所以四边形
,所以四边形![]() 的面积
的面积![]()
 ,.
,.
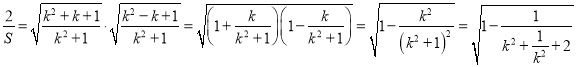
∵ ![]() ,∴
,∴![]() .
.
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() .
.
∴ 当![]() 时,四边形
时,四边形![]() 的面积最大值为
的面积最大值为![]() .
.
(3) 曲线![]() 的方程为
的方程为![]() ,它关于直线
,它关于直线![]() 、
、![]() 和原点对称,
和原点对称,
下面证明:
设曲线![]() 上任一点的坐标为
上任一点的坐标为![]() ,则
,则![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,显然
,显然![]() ,所以点
,所以点![]() 在曲线
在曲线![]() 上,故曲线
上,故曲线![]() 关于直线
关于直线![]() 对称,
对称,
同理曲线![]() 关于直线
关于直线![]() 和原点对称.
和原点对称.
证明:求得![]() 和直线
和直线![]() 的交点坐标为
的交点坐标为 ,
,
![]() 和直线
和直线![]() 的交点坐标为
的交点坐标为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,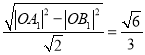 .
.
在![]() 上取点
上取点 .
.
设![]() 为曲线
为曲线![]() 上任一点,则
上任一点,则
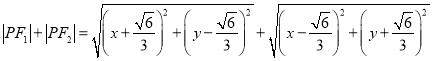
![]()
![]()
![]()

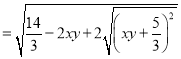
 (因为
(因为![]() )
)
![]() .
.
即曲线![]() 上任一点
上任一点![]() 到两定点
到两定点 的距离之和为定值
的距离之和为定值![]() .
.
若点![]() 到两定点
到两定点 的距离之和为定值
的距离之和为定值![]() ,可以求得点
,可以求得点![]() 的轨迹方程为
的轨迹方程为![]() (过程略).
(过程略).
故曲线![]() 是椭圆
是椭圆


科目:高中数学 来源: 题型:
【题目】将数列![]() 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
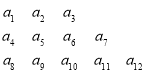
……
记表中的第一列数![]() ,
,![]() ,
,![]() ,…,构成数列
,…,构成数列![]() .
.
(1)设![]() ,求m的值;
,求m的值;
(2)若![]() ,对于任何
,对于任何![]() ,都有
,都有![]() ,且
,且![]() .求数列
.求数列![]() 的通项公式.
的通项公式.
(3)对于(2)中的数列![]() ,若上表中每一行的数按从左到右的顺序均构成公比为q(
,若上表中每一行的数按从左到右的顺序均构成公比为q(![]() )的等比数列,且
)的等比数列,且![]() ,求上表中第k(
,求上表中第k(![]() )行所有项的和
)行所有项的和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在非零实数
,若存在非零实数![]() 满足对任意
满足对任意![]() ,均有
,均有![]() ,且
,且![]() ,则称
,则称![]() 为
为![]() 上的
上的![]() 高调函数. 如果定义域为
高调函数. 如果定义域为![]() 的函数
的函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,且
,且![]() 为
为![]() 上的8高调函数,那么实数
上的8高调函数,那么实数![]() 的取值范围为____.
的取值范围为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-![]() ,x∈(0,1].
,x∈(0,1].
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在x∈(0,1]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中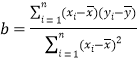 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com