
【题目】(本小题满分12分) 命题![]() 实数x满足
实数x满足![]() (其中
(其中![]() ),命题
),命题![]() 实数
实数![]() 满足
满足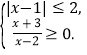
(Ⅰ)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 是
是![]()
![]() 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
【答案】(1)实数x的取值范围为(2,3);(2)实数a的取值范围是(1,2].
【解析】
本题考查复合命题的应用和必要条件、充分条件、充要条件的应用,是基础题.解题时要认真审题,仔细解答
(1)当a=1时,p真:1<x<3,q真:2<x≤4,由p∧q为真,能求出x的取值范围.
(2)若p是q的充分不必要条件,则q是p的充分不必要条件,由a>0,知p:a<x<3a,q:2<x≤4,由此能求出a的取值范围.
(Ⅰ)由![]() 得
得![]() ,又
,又![]() ,所以
,所以![]() ,
,
当![]() 时,1<
时,1<![]() ,即
,即![]() 为真时实数
为真时实数![]() 的取值范围是1<
的取值范围是1<![]() . ········· 2分
. ········· 2分
由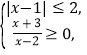 得
得![]() 解得
解得![]() ,
,
即![]() 为真时实数
为真时实数![]() 的取值范围是
的取值范围是![]() . ··················· 4分
. ··················· 4分
若![]() 为真,则
为真,则![]() 真且
真且![]() 真,所以实数
真,所以实数![]() 的取值范围是
的取值范围是![]() . ········· 6分
. ········· 6分
(Ⅱ)由(Ⅰ)知p:![]() ,则
,则![]() :
:![]() 或
或![]() ,··········· 8分
,··········· 8分
q:![]() ,则
,则![]() :
:![]() 或
或![]() ,···················· 10分
,···················· 10分
![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() ,且
,且![]() ,
,
∴![]() 解得
解得![]() ,故实数a的取值范围是
,故实数a的取值范围是![]() .··········· 12分
.··········· 12分


科目:高中数学 来源: 题型:
【题目】某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
额数 | 15 | 20 | 9 | 3 | 3 |
附:临界值表参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
(1)做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值;
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
资助超过500元 | 30 | ||
资助不超过500元 | 6 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
额数 | 15 | 20 | 9 | 3 | 3 |
附:临界值表参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
(1)做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值;
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
资助超过500元 | 30 | ||
资助不超过500元 | 6 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,假命题为( )
A. 存在四边相等的四边形不是正方形
B. z1,z2∈C,z1+z2为实数的充分必要条件是z1,z2互为共轭复数
C. 若x,y∈R,且x+y>2,则x,y至少有一个大于1
D. 对于任意n∈N+,![]() 都是偶数
都是偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z满足zi=2﹣i,i为虚数单位,
p1:|z|= ![]() ,
,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为﹣1+2i,
p4:z的虚部为2i.
其中的真命题为( )
A.p1 , p3
B.p2 , p3
C.p1 , p2
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器在一天内发生故障的概率为p.已知这台机器在3个工作日至少一天不发生故障的概率为0.999.
(1)求p;
(2)若这台机器一周5个工作日不发生故障,可获利5万元;发生一次故障任可获利2.5万元;发生2次故障的利润为0元;发生3次或3次以上故障要亏损1万元.这台机器一周内可能获利的均值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com