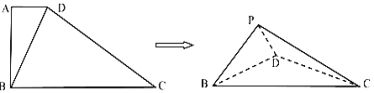
【题目】如图，在直角梯形
中，
∥
，
，
，将直角梯形沿对角线
折起，使点
到
点位置，则四面体
的体积的最大值为________，此时，其外接球的表面积为________．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知直线
与椭圆
交于不同的两点
，
.
（1）若线段
的中点为
，求直线的方程；
（2）若的斜率为
，且过椭圆
的左焦点
，的垂直平分线与
轴交于点
，求证：
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1：乙套设备的样本的频率分布直方图
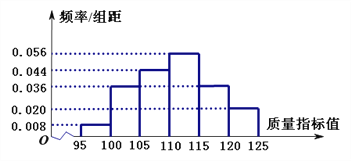
（Ⅰ）将频率视为概率. 若乙套设备生产了5000件产品，则其中的不合格品约有多少件；
（Ⅱ）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（Ⅲ）根据表1和图1，对两套设备的优劣进行比较.
附：
.
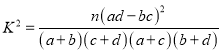查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系 xOy 中，已知椭圆 C：
＝1(a>b>0)的离心率为
，且过点
，点P在第四象限， A为左顶点， B为上顶点， PA交y轴于点C，PB交x轴于点D.
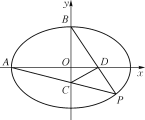
(1) 求椭圆 C 的标准方程；
(2) 求 △PCD 面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据国家统计局发布的数据，2019年11月全国CPI（居民消费价格指数），同比上涨4.5%，CPI上涨的主要因素是猪肉价格的上涨，猪肉加上其他畜肉影响CPI上涨3.27个百分点．下图是2019年11月CPI一篮子商品权重，根据该图，下列结论错误的是（ ）
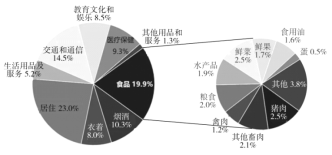
A.CPI一篮子商品中所占权重最大的是居住
B.CPI一篮子商品中吃穿住所占权重超过50%
C.猪肉在CPI一篮子商品中所占权重约为2.5%
D.猪肉与其他畜肉在CPI一篮子商品中所占权重约为0.18%
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4 — 4：坐标系与参数方程
在直角坐标系
中，直线
的参数方程为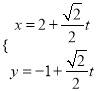
（
为参数），以原点为极点， 
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
（
）．
（1）分别写出直线
的普通方程与曲线
的直角坐标方程；
（2）已知点
，直线
与曲线
相交于
两点，若
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某数学小组从医院和气象局获得2018年1月至6月份每月20的昼夜温差
，（
）和患感冒人数（
/人）的数据，画出如图的折线图.
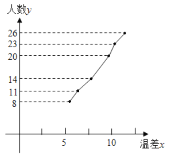
（1）建立关于
的回归方程（精确到0.01），预测2019年1月至6月份昼夜温差为
时患感冒的人数（精确到整数）；
（2）求与的相关系数，并说明与的相关性的强弱（若
，则认为与具有较强的相关性），
参考数据：
，
，
，
，
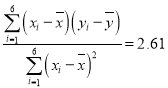相关系数：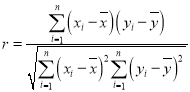
，回归直线方程是
，
，
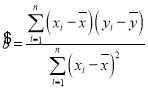查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
