已知二次函数y=f(x),满足f(-2)=f(0)=0,且f(x)的最小值为-1.
(1)若函数y=F(x),x∈R为奇函数,当x>0时,F(x)=f(x),求函数y=F(x),x∈R的解析式;
(2)设g(x)=f(-x)-λf(x)+1,若g(x)在[-1,1]上是减函数,求实数λ的取值范围.
【答案】
分析:(1)由f(-2)=f(0)可知函数的对称轴x=-1,结合f(x)的最小值为-1可设f(x)=a(x+1)
2-1
然后代入f(0)=0可求a,结合函数y=F(x)为奇函数及x>0时,F(x)=f(x)可求F(x)
(2)代入整理求出g(x),分类讨论函数g(x)为一次函数及二次函数两种情况分别 讨论即可求解
解答:解:(1)∵f(-2)=f(0)=0,
∴函数的对称轴x=-1
∵f(x)的最小值为-1.
由题意可设f(x)=a(x+1)
2-1
∵f(0)=a-1=0
∴a=1
∴f(x)=x
2+2x
∵y=F(x)为奇函数,
∴F(0)=0
∵当x>0时,F(x)=f(x)=x
2+2x
∴x<0时,-x>0
∴F(-x)=(-x)
2+2(-x)=x
2-2x
∴F(x)=-(-x)=-x
2+2x
F(x)=
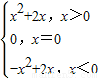
(2)∵g(x)=f(-x)-λf(x)+1=x
2-2x-λ(x
2+2x)+1
=(1-λ)x
2-2(1+λ)x+1
若g(x)在[-1,1]上是减函数
①若1-λ=0即λ=1时,g(x)=-4x+1在[-1,1]上单调递减,满足题意
②若1-λ<0即λ>1时,g(x)=(1-λ)x
2-2(1+λ)x+1是开口向下的抛物线,对称轴x=

则由题意可得

∴λ>1满足题意
③若1-λ>0即λ<1时,g(x)=(1-λ)x
2-2(1+λ)x+1是开口向上的抛物线,对称轴x=

∴

∴0≤λ<1
综上可得,λ≥0
点评:本题主要考查了利用二次函数的性质求解函数的解析式及函数的奇偶性在求解中的应用,一次函数与二次函数的单调性的应用,具有一定的综合性

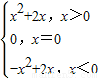






 阅读快车系列答案
阅读快车系列答案 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: