练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】十九大以来，国家深入推进精准脱贫，加大资金投入，强化社会帮扶，为了更好的服务于人民，派调查组到某农村去考察和指导工作.该地区有200户农民，且都从事水果种植，据了解，平均每户的年收入为3万元.为了调整产业结构，调查组和当地政府决定动员部分农民从事水果加工，据估计，若能动员户农民从事水果加工，则剩下的继续从事水果种植的农民平均每户的年收入有望提高，而从事水果加工的农民平均每户收入将为万元.

    （1）若动员户农民从事水果加工后，要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入，求的取值范围；

    （2）在（1）的条件下，要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入，求的最大值.

    【答案】（1）；（2）

    【解析】

    （1）求得从事水果种植的农民的总年收入，由此列不等式，解不等式求得的取值范围.

    （2）从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入列不等式，根据分离常数法求得的取值范围，由此求得的最大值.

    （1）动员户农民从事水果加工后，要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入，则，解得.

    （2）由于从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入，则，（），

    化简得，（）.

    由于，当且仅当时等号成立，所以，所以的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在“新零售”模式的背景下，某大型零售公司为推广线下分店，计划在S市的A区开设分店．为了确定在该区开设分店的个数，该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格．记x表示在各区开设分店的个数，y表示这x个分店的年收入之和．

    x（个）

    2

    3

    4

    5

    6

    y（百万元）

    2.5

    3

    4

    4.5

    6

    (1)该公司经过初步判断，可用线性回归模型拟合y与x的关系，求y关于x的线性回归方程；

    （2）假设该公司在A区获得的总年利润z（单位：百万元）与x，y之间满足的关系式为：,请结合（1）中的线性回归方程，估算该公司应在A区开设多少个分店，才能使A区平均每个分店的年利润最大？

    附：回归方程中的斜率和截距的最小二乘估计公式分别为：

    ， .

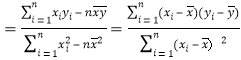    （参考数据：，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|ax2+2x+1=0，a∈R}，

    （1）若A只有一个元素，试求a的值，并求出这个元素；

    （2）若A是空集，求a的取值范围；

    （3）若A中至多有一个元素，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月27日当今世界围棋排名第一的柯洁在与的人机大战中中盘弃子认输，至此柯洁与的三场比赛全部结束，柯洁三战全负，这次人机大战再次引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查，根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

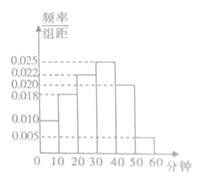
    （1）请根据已知条件完成下面列联表，并据此资料你是否有95%的把握认为“围棋迷”与性别有关？

    非围棋迷

    围棋迷

    合计

    男

    女

    10

    55

    合计

    （2）将上述调查所得到的频率视为概率，现在从该地区大量学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名学生中的“围棋迷”人数为，若每次抽取的结果是相互独立的，求的分布列，数学期望和方差.

    独立性检查临界值表：

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    …

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    …

    （参考公式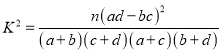： ，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某农科所发现，一种作物的年收获量（单位：）与它“相近”作物的株数具有相关关系（所谓两株作物“相近”是指它们的直线距离不超过），并分别记录了相近作物的株数为时，该作物的年收获量的相关数据如下：

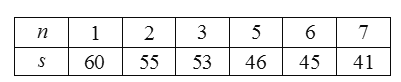
    （1）根据研究发现，该作物的年收获量可能和它“相近”作物的株数有以下两种回归方程：，利用统计知识，结合相关系数比较使用哪种回归方程更合适；

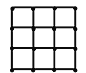
    （2）农科所在如下图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每个小正方形的面积为，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望.（注：年收获量以（1）中选择的回归方程计算所得数据为依据）

    参考公式：线性回归方程为，其中，，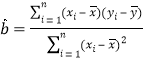

    相关系数；

    参考数值：，，，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为担任班主任的教师办理手机语音月卡套餐，为了解通话时长，采用随机抽样的方法，得到该校100位班主任每人的月平均通话时长（单位：分钟）的数据，其频率分布直方图如图所示，将频率视为概率.

    （1）求图中的值；

    （2）估计该校担任班主任的教师月平均通话时长的中位数；

    （3）在，这两组中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求抽取的2人恰在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面，在中，，为的中点，四边形是等腰梯形，，．

    （Ⅰ）求异面直线与所成角的正弦值；

    （Ⅱ）求证：平面平面；

    （Ⅲ）求直线与平面所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为，以坐标原点为极点，轴非负半轴为极轴建立极坐标系，点为曲线上的动点，点在线段 的延长线上，且满足，点的轨迹为.

    （1）求曲线，的极坐标方程；

    （2）设点的极坐标为，求面积的最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的四棱锥中，底面为矩形， ， 的中点为, ，异面直线与所成的角为， 平面.

    （1）证明： 平面；

    （2）求二面角的余弦值的大小.

    查看答案和解析>>

    同步练习册答案