
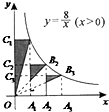
 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$. 分析 根据反比例函数的比例系数k的几何意义得到第1个阴影三角形的面积=4,由于第2个阴影三角形与三角形OB2C2相似,根据相似得性质得则第2个阴影三角形的面积=$\frac{1}{4}$S△OB2C2=($\frac{1}{2}$)2×$\frac{1}{2}$×8=$\frac{4}{4}$,同理可得第3个阴影三角形的面积,即可求出阴影部分的面积之和.
解答 解:第1个阴影三角形的面积=$\frac{1}{2}$×8=4,
第2个阴影三角形的面积=$\frac{1}{4}$S△OB2C2=($\frac{1}{2}$)2×$\frac{1}{2}$×8=$\frac{4}{4}$,
第3个阴影三角形的面积=$\frac{1}{9}$S△OB3C3=($\frac{1}{3}$)2×$\frac{1}{2}$×8=$\frac{4}{9}$,
所以图中阴影部分的面积之和为4(1+$\frac{1}{4}$+$\frac{1}{9}$)=$\frac{49}{9}$.
故答案为:$\frac{49}{9}$.
点评 本题考查了反比例函数的比例系数k的几何意义,考查了相似三角形面积的比等于相似比的平方,考查学生分析解决问题的能力,属于中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | y2=6x | C. | y2=8x | D. | y2=9x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 135° | C. | 45° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com