
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 和曲线
和曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() .
.
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
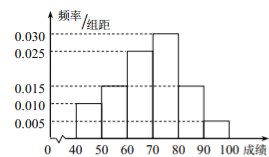
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
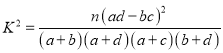 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
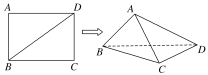
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
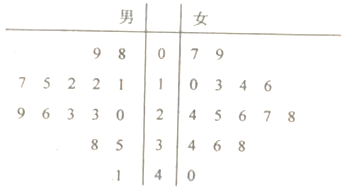
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
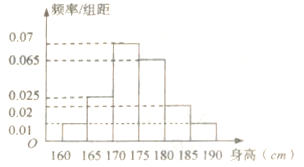
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com