【题目】南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式：“以小斜幂并大斜幂，减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减之，以四约之，为实，一为从隅，开方得积．”（即：S＝
，a＞b＞c），并举例“问沙田一段，有三斜（边），其小斜一十三里，中斜一十四里，大斜一十五里，欲知为田几何?”则该三角形田面积为
A. 82平方里 B. 84平方里
C. 85平方里 D. 83平方里
科目：高中数学 来源： 题型：
【题目】设事件A表示“关于
的一元二次方程
有实根”，其中
， 
为实常数.
（Ⅰ）若
为区间[0，5]上的整数值随机数， 
为区间[0，2]上的整数值随机数，求事件A发生的概率；
（Ⅱ）若
为区间[0，5]上的均匀随机数， 
为区间[0，2]上的均匀随机数，求事件A发生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义域为R的奇函数f（x）满足f（4﹣x）+f（x）=0，当﹣2＜x＜0时，f（x）=2x ， 则f（log220）=（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝
，g（x）＝
，若函数y＝f（g（x））＋a有三个不同的零点x1，x2，x3（其中x1＜x2＜x3），则2g（x1）＋g（x2）＋g（x3）的取值范围为______．
【答案】
【解析】
首先研究函数
和函数
的性质，然后结合韦达定理和函数的性质求解2g（x1）＋g（x2）＋g（x3）的取值范围即可.
由题意可知：
，
将对勾函数
的图象向右平移一个单位，再向上平移一个单位即可得到函数的图象，其图象如图所示：
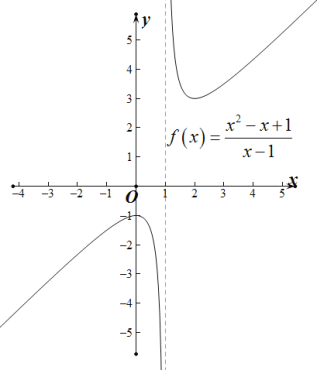
由
可得
，
据此可知在区间
上单调递增，在区间
上单调递减，
绘制函数图象如图所示：
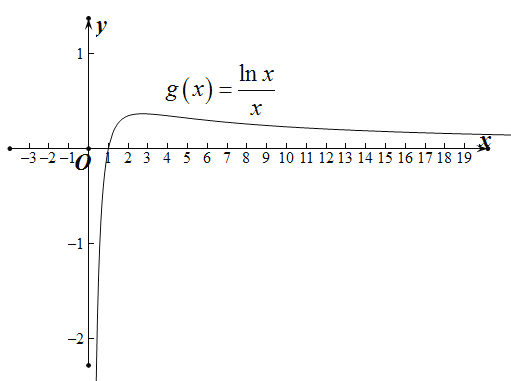
则的最大值为
，
，
函数y＝f（g（x））＋a有三个不同的零点，则
，
令
，则
，
整理可得：
，由韦达定理有：
.
满足题意时，应有：
，
，
故
.
【点睛】
本题主要考查导数研究函数的性质，等价转化的数学思想，复合函数的性质及其应用等知识，意在考查学生的转化能力和计算求解能力.
【题型】填空题
【结束】
17
【题目】已知等比数列{
}的前n项和为
，且满足2＝
＋m（m∈R）．
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若数列{
}满足
，求数列{}的前n项和
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有6个人排成一排照相，由于甲乙性格不合，所以要求甲乙不相邻，丙最高，要求丙站在最中间的两个位置中的一个位置上，则不同的站法有（ ）种.
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=lnx+x2﹣ax，a∈R
（1）若f（x）在P（x0 ， y0）（x∈[ 
））处的切线方程为y=﹣2，求实数a的值；
（2）若x1 ， x2（x1＜x2）是函数f（x）的两个零点，f′（x）是函数f（x）的导函数，证明：f′（ 
）＜0．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
