练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．下列推理中属于类比推理的是（　　）
    A．一切偶数都能被2整除，2100是偶数，所以2100能被2整除．
    B．由a1，a2，a3…，归纳出数列的通项公式an
    C．由平面三角形的性质，推测空间四边形的性质
    D．如果a＞b，c＞d，则a-d＞b-c

    分析 利用归纳推理、类比推理和演绎推理的定义进行判断，即可得出结论．

    解答 解：A，一切偶数都能被2整除，.2100是偶数，所以2100能被2整除，为演绎推理；
    B，由a1，a2，a3…，归纳出数列的通项公式an，是归纳推理；
    C，由平面三角形的性质，推测空间四面体的性质，为类比推理；
    D，如果a＞b，c＞d，则a-d＞b-c，为演绎推理．
    故选：C．

    点评 本题考查的知识点是类比推理，熟练掌握归纳推理、类比推理和演绎推理的定义，是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．设y=$\frac{ln（3x+14）}{x}$，则y′|x=-1=-（$\frac{3}{11}+ln11$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．1.2log6$\sqrt{2}$+3log6$\root{3}{3}$=（　　）
    A．0B．1C．6D．log6$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若一位学生把英语单词“error”中字母的拼写错了，则可能出现错误的种数是（　　）
    A．9B．10C．19D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如图所示是一个有n层（n≥2，n∈N*）的六边形点阵，它的中心是一个点，算作第1层，第2层每边有2个点，第3层每边有3个点，…，第n层每边有n个点，则这个点阵共有（　　）个点．
    A．n2B．n2+nC．3n2-3n+1D．3n2-3n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）在[a，b]上有定义，若对任意x1，x2∈[a，b]，有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{1}{2}[f（{x_1}）+f（{x_2}）]$，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
    ①f（x）在[1，3]上的图象是连续不断的；
    ②f（x2）在$[1，\;\sqrt{3}]$上具有性质P；
    ③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
    ④任意x1，x2，x3，x4∈[1，3]，有$f（\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}）≤\frac{1}{4}[f（{x_1}）+f（{x_2}）+f（{x_3}）+f（{x_4}）]$．
    其中真命题的序号是（　　）
    A．①②B．①③C．②④D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的焦点坐标为（　　）
    A．（±$\sqrt{7}$，0）B．（0，±$\sqrt{7}$）C．（±5，0）D．（0，±5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．设数列{an}的前n项和S由如下程序框图给出，若输入n的值为100，求输出的S．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

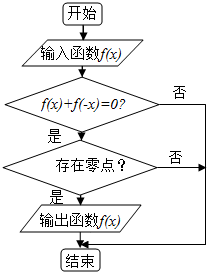    13．某程序框图如图所示，现输入如下四个函数，其中可以输出的函数是f（x）=sinx．
    A、f（x）=x2
    B、f（x）=$\frac{1}{x}$
    C、f（x）=lnx+2x-6
    D、f（x）=sinx．

    查看答案和解析>>

    同步练习册答案