
【题目】设函数f(x)=ex+sinx,g(x)=ax,F(x)=f(x)﹣g(x).
(1)若x=0是F(x)的极值点,求a的值;
(2)当 a=1时,设P(x1 , f(x1)),Q(x2 , g(x2))(x1>0,x2>0),且PQ∥x轴,求P、Q两点间的最短距离;
(3)若x≥0时,函数y=F(x)的图象恒在y=F(﹣x)的图象上方,求实数a的取值范围.
【答案】
(1)解: F(x)=ex+sinx﹣ax,F′(x)=ex+cosx﹣a.
因为x=0是F(x)的极值点,所以F′(0)=1+1﹣a=0,a=2.
又当a=2时,若x<0,F'(x)=ex+cosx﹣a<0;若x>0,F'(x)=ex+cosx﹣a>0.
∴x=0是F(x)的极小值点,
∴a=2符合题意.
(2)解:∵a=1,且PQ∥x轴,由f(x1)=g(x2)得: ![]() ,
,
所以 ![]() .
.
令h(x)=ex+sinx﹣x,h′(x)=ex+cosx﹣1>0,当x>0时恒成立.
∴x∈[0,+∞)时,h(x)的最小值为h(0)=1.
∴|PQ|min=1.
(3)解:令φ(x)=F(x)﹣F(﹣x)=ex﹣e﹣x+2sinx﹣2ax.
则φ′(x)=ex+e﹣x+2cosx﹣2a.S(x)=φ′′(x)=ex﹣e﹣x﹣2sinx.
因为S′(x)=ex+e﹣x﹣2cosx≥0当x≥0时恒成立,
所以函数S(x)在[0,+∞)上单调递增,
∴S(x)≥S(0)=0当x∈[0,+∞)时恒成立;
因此函数φ′(x)在[0,+∞)上单调递增,φ′(x)≥φ′(0)=4﹣2a当x∈[0,+∞)时恒成立.
当a≤2时,φ′(x)≥0,φ(x)在[0,+∞)单调递增,即φ(x)≥φ(0)=0.
故a≤2时F(x)≥F(﹣x)恒成立.
【解析】(1)、根据题意先求出函数F(x)的函数表达式,再求出其导函数F′(x),令F′(0)=0便可求出a的值;(2)、根据题意可知(x1)=g(x2),令h(x)=x2﹣x1=ex+sinx﹣x,求出其导函数,进而求得h(x)的最小值即为P、Q两点间的最短距离;(3)、令φ(x)=F(x)﹣F(﹣x),求出其导函数,便可求出φ(x)的单调性,进而可求得a的取值范围.
【考点精析】本题主要考查了函数的极值的相关知识点,需要掌握极值反映的是函数在某一点附近的大小情况才能正确解答此题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】设圆![]() ,直线
,直线![]() .
.
(1)求证: ![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)设![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,求弦
,求弦![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)若点![]() 分弦
分弦![]() 所得的向量满足
所得的向量满足![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题:

(1)写出从药物释放开始,每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4人去旅游,旅游地点有A,B两个地方可以选择,但4人都不知道去哪里玩,于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩,掷出能被3整除的数时去A地,掷出其他的则去B地.
(1)求这4个人恰好有1个人去A地的概率;
(2)用X,Y分别表示这4个人中去A,B两地的人数,记ξ=XY,求随机变量ξ的分布列与数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高级中学在今年“五一”期间给校内所有教室安装了同一型号的空调,关于这批空调的使用年限![]() 单位:年
单位:年![]() 和所支出的维护费用
和所支出的维护费用![]() 单位:千元
单位:千元![]() 厂家提供的统计资料如表:
厂家提供的统计资料如表:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
![]() 若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程
若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程![]() ;
;
![]() 若规定当维护费用y超过
若规定当维护费用y超过![]() 千元时,该批空调必须报度,试根据
千元时,该批空调必须报度,试根据![]() 的结论求该批空调使用年限的最大值
的结论求该批空调使用年限的最大值![]() 结果取整数
结果取整数![]() 参考公式:
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,AC=BC=AB=2,AA1=3,D点是AB的中点
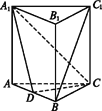
(1)求证:BC1∥平面CA1D.
(2)求三棱锥B-A1DC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=x2﹣x+alnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证f(x2)< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com