
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
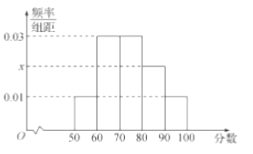
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求![]() 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率.
【答案】(1)见解析;(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)由各个矩形的面积和为![]() 可得
可得![]() ,各矩形中点横坐标对应频率之积求和即可得平均数,设中位数为
,各矩形中点横坐标对应频率之积求和即可得平均数,设中位数为![]() 分,利用
分,利用![]() 左右两边面积为
左右两边面积为![]() 可得中位数;(2)根据直方图可得50名学生中成绩不低于70分的频率,即可估计这次测试成绩不低于70分的人数;(3)利用列举法,确定基本事件的个数,即利用古典概型概率公式可求出两组中至少有1人被抽到的概率的概率.
可得中位数;(2)根据直方图可得50名学生中成绩不低于70分的频率,即可估计这次测试成绩不低于70分的人数;(3)利用列举法,确定基本事件的个数,即利用古典概型概率公式可求出两组中至少有1人被抽到的概率的概率.
试题解析:(1)由频率分布直方图可得第4组的频率为![]()
![]() ,
,
故![]() .
.
故可估计所抽取的50名学生成绩的平均数为
![]()
![]()
![]() (分).
(分).
由于前两组的频率之和为![]() ,前三组的频率之和为
,前三组的频率之和为![]() ,故中位数在第3组中.
,故中位数在第3组中.
设中位数为![]() 分,
分,
则有![]() ,所以
,所以![]() ,
,
即所求的中位数为![]() 分.
分.
(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,
,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为![]() .
.
(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
, ![]() ,
, ![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
, ![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共20种.
共20种.
其中![]() 两组中没有人被抽到的可能结果为
两组中没有人被抽到的可能结果为![]() ,只有1种,
,只有1种,
故![]() 两组中至少有1人被抽到的概率为
两组中至少有1人被抽到的概率为![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 命题![]() 的否定是:
的否定是:![]()
B. 命题![]() 中,若
中,若![]() ,则
,则![]() 的否命题是真命题
的否命题是真命题
C. 如果![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() 为真命题,
为真命题,![]() 为假命题
为假命题
D. ![]() 是函数
是函数![]() 的最小正周期为
的最小正周期为![]() 的充分不必要条件
的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足以下三个条件:
满足以下三个条件:
①对任意实数![]() ,都有
,都有![]() ;
;
②![]() ;
;
③![]() 在区间
在区间![]() 上为增函数.
上为增函数.
(1)判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)求证:![]() ;
;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求
相切,求![]() 的值;
的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数
对于任意正实数![]() 恒成立,当
恒成立,当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,坐标原点为
,坐标原点为![]() .椭圆
.椭圆![]() 的动弦
的动弦![]() 过右焦点
过右焦点![]() 且不垂直于坐标轴,
且不垂直于坐标轴,![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]() .
.
(I)求点![]() 的横坐标;
的横坐标;
(II)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)=|x2﹣ax|(a∈R),设g(x)=f(x+l)﹣f(x).
(1)若y=g(x)为奇函数,求a的值:
(2)设h(x)![]() ,x∈(0,+∞)
,x∈(0,+∞)
①若a≤0,证明:h(x)>2:
②若h(x)的最小值为﹣1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com