
【题目】已知圆![]() 的一条直径是椭圆
的一条直径是椭圆![]() 的长轴,过椭圆
的长轴,过椭圆![]() 上一点
上一点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于点
相交于点![]() ,弦
,弦![]() 的最小值为
的最小值为![]() .
.
(1)求圆![]() 及椭圆
及椭圆![]() 的方程;
的方程;
(2) 已知点![]() 是椭圆
是椭圆![]() 上的任意一点,点
上的任意一点,点![]() 是
是![]() 轴上的一定点,直线
轴上的一定点,直线![]() 的方程为
的方程为![]() ,若点
,若点![]() 到定直线
到定直线![]() 的距离与到定点
的距离与到定点![]() 的距离之比为
的距离之比为![]() ,求定点
,求定点![]() 的坐标.
的坐标.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
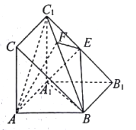
【题目】如图,直三棱柱ABC—A1B1C1中,侧面AA1B1B是正方形,AC丄侧面AA1B1B,AC=AB,点E是B1C1的中点.
(Ⅰ)求证:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足为F,求二面角B—AF—A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
(t为参数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程,并指明曲线C的形状;
(Ⅱ)设直线l与曲线C交于A,B两点,O为坐标原点,且|OA|<|OB|,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
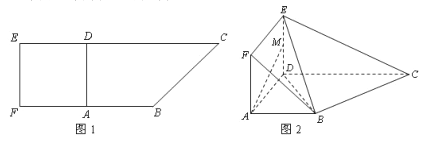
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 是定义在
是定义在![]() 上的不恒为零的函数,对于任意实数
上的不恒为零的函数,对于任意实数![]() 满足:
满足: ![]() ,
,![]()
![]() ,
,![]() 考查下列结论:①
考查下列结论:①![]() ;②
;②![]() 为奇函数;③数列
为奇函数;③数列![]() 为等差数列;④数列
为等差数列;④数列![]() 为等比数列.
为等比数列.
以上结论正确的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com