
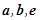 及实数
及实数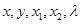 ,给出下列四个条件:
,给出下列四个条件: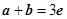 且
且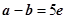 ; ②
; ②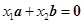
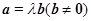 且
且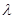 唯一; ④
唯一; ④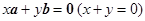
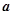 与
与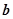 共线的是
共线的是 | A.①② | B.②④ | C.①③ | D.③④ |
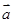 ="-4"
="-4" 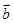 ,故
,故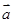 与
与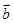 共线,故①满足条件.
共线,故①满足条件.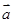 与
与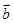 为任意向量,故②不满足条件.
为任意向量,故②不满足条件.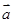 与
与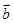 共线,故③满足条件.
共线,故③满足条件.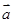 与
与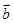 一定共线.
一定共线.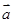 +
+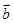 =3
=3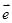 ,
,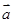 -
-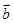 =g
=g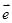 ,解得
,解得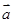 = 4
= 4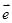 ,
,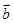 = -
= -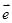 ,
,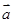 =-4
=-4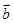 ,故
,故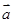 与
与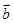 共线,故①满足条件.
共线,故①满足条件.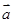 与
与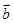 为任意向量,不能推出
为任意向量,不能推出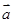 与
与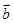 一定共线,故②不满足条件.
一定共线,故②不满足条件.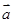 ="λ" ?
="λ" ?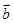 ,∴
,∴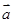 与
与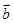 共线,故③满足条件.
共线,故③满足条件.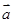 与
与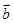 一定共线,故②不满足条件.
一定共线,故②不满足条件.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com