
【题目】设函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:解含参的一元二次不等式,当二次项系数含参时,首先讨论二次项的系数,特别是不能忘记二次项系数为0的情况,当二次项的系数不为0时,分二次项系数大于0,和小于0两种情况,比较两根的大小,根据不等式的要求写出不等式的解集;分离参数法求参数的取值范围也是常见题型,首先分离参数,注意不等号的方向,求最值,利用“极值原理”求最值,给出参数的取值范围.
试题解析:
(1)若![]() ,原不等式可化为
,原不等式可化为![]() ,解得
,解得![]() ;
;
若![]() ,原不等式可化为
,原不等式可化为![]() ,解得
,解得![]() 或
或![]() ;
;
若![]() ,原不等式可化为
,原不等式可化为![]() ,其解得情况应由
,其解得情况应由![]() 与
与![]() 的大小关系确定,
的大小关系确定,
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,解得
时,解得![]() .
.
综上所述,当![]() 时,解集为
时,解集为![]() 或
或![]() ;
;
当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为;
时,解集为;
当![]() 时,解集为
时,解集为![]() .
.
(2)由![]() 得
得![]()
![]()
![]()
![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立
上恒成立
令![]() ,则只需
,则只需![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时等式成立.
时等式成立.
![]() .
.


科目:高中数学 来源: 题型:
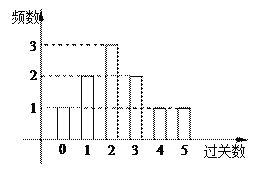
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
(Ⅰ)求小明在这十次游戏中所得奖品数的均值;
(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;
(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;
其中正确的结论是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得到曲线
倍,得到曲线![]()
(1)求出![]() 的普通方程;
的普通方程;
(2)设直线![]() :
: ![]() 与
与![]() 的交点为
的交点为![]() ,
, ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( ) 
A.14
B.10
C.7
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com