
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有100户农民,且都从事水果种植,据了解,平均每户的年收入为2万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时额定,需要确定加工零件所花费的时间,为此作了![]() 次试验,得到数据如下:
次试验,得到数据如下:
零件数 | 10 | 20 | 30 | 40 | 50 | 60 |
加工时间 | 64 | 70 | 77 | 82 | 90 | 97 |
(1)试对上述变量![]() 与
与![]() 的关系进行相关性检验,如果
的关系进行相关性检验,如果![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)根据(1)的结论,你认为每小时加工零件的数量额定为多少(四舍五入为整数)比较合理?
附:相关性检验的临界值表
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
4 | 0.811 | 0.917 |
5 | 0.754 | 0.874 |
6 | 0.707 | 0.834 |

 ,
,![]()
参考数据:![]() ;
;![]()
|
|
|
|
|
17950 | 9100 | 39158 | 1750 | 758 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.
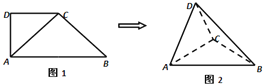
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,E,F是AD,BD中点,![]() ,
,![]() ,将
,将![]() 沿对角线BD折起至
沿对角线BD折起至![]() ,使平面
,使平面![]() 平面BCD,则四面体
平面BCD,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )

A.![]() 平面
平面![]()
B.异面直线CD与![]() 所成的角为
所成的角为![]()
C.异面直线EF与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面BCD所成的角为
与平面BCD所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.

(1)根据直方图估计这个开学季内市场需求量![]() 的平均数和众数;
的平均数和众数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)以需求量的频率作为各需求量的概率,求开学季利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张强同学进行三次定点投篮测试,已知第一次投篮命中的概率为![]() ,第二次投篮命中的概率为
,第二次投篮命中的概率为![]() ,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为
,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为![]() ,否则为
,否则为![]() .
.
(1)求张强同学三次投篮至少命中一次的概率;
(2)记张强同学三次投篮命中的次数为随机变量![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,给出下述四个结论:
,给出下述四个结论:
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②将函数![]() 的图象向左平移
的图象向左平移![]() 所得图象关于原点对称;
所得图象关于原点对称;
③函数![]() 在区间
在区间![]() ,上单调递增;
,上单调递增;
④函数![]() 在区间
在区间![]() 上有
上有![]() 个零点.
个零点.
其中所有正确结论的编号是( )
A.①②B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为促进全面健身运动,某地跑步团体对本团内的跑友每周的跑步千米数进行统计,随机抽取的100名跑友,分别统计他们一周跑步的千米数,并绘制了如图频率分布直方图.
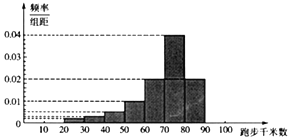
(1)由频率分布直方图计算跑步千米数不小于70千米的人数;
(2)已知跑步千米数在![]() 的人数是跑步千米数在
的人数是跑步千米数在![]() 的
的![]() ,跑步千米数在
,跑步千米数在![]() 的人数是跑步千米数在
的人数是跑步千米数在![]() 的
的![]() ,现在从跑步千米数在
,现在从跑步千米数在![]() 的跑友中抽取3名代表发言,用
的跑友中抽取3名代表发言,用![]() 表示所选的3人中跑步千米数在
表示所选的3人中跑步千米数在![]() 的人数,求
的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com