
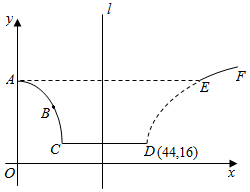
 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$分析 (1)根据C,D关于直线l对称写出C点坐标,再把A、B、C的坐标代入解析式,得到关于a,b,φ的方程组,解此方程组即得:a=6,b=19,φ=$\frac{5π}{6}$,.于是可写出ABC段的解析式,由对称性得,也可得到DEF段的解析式,最后由解析式得出何时y值最大,从而得到当x=92时,股价见顶.
(2)由(1)可知,yF=6+19=25,故可计算出这次操作老王能赚多少元.
解答 解:(1)点C、D关于直线L对称,
∴C点坐标为(2×34-44,16)即(24,16),
把A、B和C的坐标代入解析式,得$\left\{\begin{array}{l}{22=asinφ+b}\\{19=asin(\frac{π}{6}+φ)+b}\\{16=asin(\frac{π}{3}+φ)+b}\end{array}\right.$ ①
∴a[sin($\frac{π}{6}$+φ)-sinφ]=-3,a[sin($\frac{π}{3}$+φ)-sinφ]=-6
∴2sin($\frac{π}{6}$+φ)-2sinφ=sin($\frac{π}{3}$+φ)-sinφ,
∴cosφ+$\sqrt{3}$sinφ=$\frac{\sqrt{3}}{2}$cosφ+$\frac{3}{2}$sinφ,
∴(1-$\frac{\sqrt{3}}{2}$)cosφ=($\frac{3}{2}$-$\sqrt{3}$)sinφ=$\sqrt{3}$($\frac{\sqrt{3}}{2}$-1)sinφ,
∴tanφ=-$\frac{\sqrt{3}}{3}$,
0<φ<π,
∴φ=π-$\frac{π}{6}$=$\frac{5π}{6}$,
代入①求得b=19,a=6,
∴a=6,b=19,φ=$\frac{5π}{6}$,
于是ABC段的解析式为y=6sin($\frac{π}{72}$x+$\frac{5π}{6}$)+19,由对称=6性得
DEF段的解析式为y=6sin[$\frac{π}{72}$(68-x)+$\frac{5π}{6}$]+19,
∴$\frac{π}{72}$(68-xF)+$\frac{5π}{6}$=$\frac{π}{2}$,\,解得xF=92,
∴当x=92时,股价见顶.
(2)由(1)可知,yF=6+19=25,故这次操作老张能赚3000×(25-16)=27000(元)
点评 本题主要考查了在实际问题中建立三角函数模型,体现了数学在实际生活中的应用,解答关键是数形结合法的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y=\frac{1}{x}$ | C. | y=-tanx | D. | y=-x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$a2 | B. | -$\frac{1}{2}$a2 | C. | a2 | D. | -a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com