已知函数f(x)=lnx+ax2+bx(其中a,b)为常数且a≠0)在x=1处取得极值.
(I) 当a=1时,求f(x)的单调区间;
(II) 若f(x)在(0,e]上的最大值为1,求a的值.
解:(I)因为f(x)=lnx+ax
2+bx所以f′(x)=

+2ax+b,…(2分)
因为函数f(x)=lnx+ax
2+bx在x=1处取得极值
f′(1)=1+2a+b=0…(3分)
当a=1时,b=-3,f′(x)=
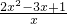
,
f′(x),f(x)随x的变化情况如下表:
| x | (0, ) ) |  | ( ,1) ,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
…(5分)
所以f(x)的单调递增区间为(0,

),(1,+∞)
单调递减区间为(

,1)…(6分)
(II)因为f′(x)=
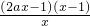
令f′(x)=0,x
1=1,x
2=

…(7分)
因为f(x)在 x=1处取得极值,所以x
2=

≠x
1=1,
当

<0时,f(x)在(0,1)上单调递增,在(1,e]上单调递减
所以f(x)在区间(0,e]上的最大值为f(1),
令f(1)=1,解得a=-2…(9分)
当a>0,x
2=

>0
当

<1时,f(x)在(0,

)上单调递增,(

,1)上单调递减,(1,e)上单调递增
所以最大值1可能在x=

或x=e处取得
而f(

)=ln

+a(

)
2-(2a+1)

=ln

-

<0
所以f(e)=lne+ae
2-(2a+1)e=1,解得a=
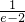
…(11分)
当1≤

<e时,f(x)在区间(0,1)上单调递增,(1,

)上单调递减,(

,e)上单调递增
所以最大值1可能在x=1或x=e处取得
而f(1)=ln1+a-(2a+1)<0
所以f(e)=lne+ae
2-(2a+1)e=1,
解得a=
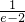
,与1<x
2=

<e矛盾…(12分)
当x
2=

≥e时,f(X)在区间(0,1)上单调递增,在(1,e)单调递减,
所以最大值1可能在x=1处取得,而f(1)=ln1+a-(2a+1)<0,矛盾
综上所述,a=
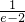
或a=-2.…(13分)
分析:(I)由函数的解析式,可求出函数导函数的解析式,进而根据x=1是f(x)的一个极值点f′(1)=0,可构造关于a,b的方程,根据a=1求出b值;可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数f(x)的单调区间;
(II)对函数求导,写出函数的导函数等于0的x的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于a的方程求得结果.
点评:本题考查的知识点是利用导数研究函数的极值,利用导数研究函数的单调性,以及利用导数研究函数在闭区间上的最值,其中根据已知条件确定a,b值,得到函数导函数的解析式并对其符号进行分析,是解答的关键.属于中档题.

 +2ax+b,…(2分)
+2ax+b,…(2分)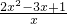 ,
, )
)
 ,1)
,1) ),(1,+∞)
),(1,+∞) ,1)…(6分)
,1)…(6分)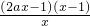
 …(7分)
…(7分) ≠x1=1,
≠x1=1, <0时,f(x)在(0,1)上单调递增,在(1,e]上单调递减
<0时,f(x)在(0,1)上单调递增,在(1,e]上单调递减 >0
>0 <1时,f(x)在(0,
<1时,f(x)在(0, )上单调递增,(
)上单调递增,( ,1)上单调递减,(1,e)上单调递增
,1)上单调递减,(1,e)上单调递增 或x=e处取得
或x=e处取得 )=ln
)=ln +a(
+a( )2-(2a+1)
)2-(2a+1) =ln
=ln -
- <0
<0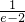 …(11分)
…(11分) <e时,f(x)在区间(0,1)上单调递增,(1,
<e时,f(x)在区间(0,1)上单调递增,(1, )上单调递减,(
)上单调递减,( ,e)上单调递增
,e)上单调递增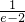 ,与1<x2=
,与1<x2= <e矛盾…(12分)
<e矛盾…(12分) ≥e时,f(X)在区间(0,1)上单调递增,在(1,e)单调递减,
≥e时,f(X)在区间(0,1)上单调递增,在(1,e)单调递减,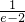 或a=-2.…(13分)
或a=-2.…(13分)
