
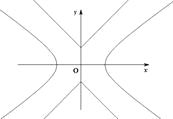
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
【答案】见解析
【解析】
(1)C1的左焦点为![]() ,过F的直线
,过F的直线![]() 与C1交于
与C1交于![]() ,与C2交于
,与C2交于![]() ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为![]() ;
;
(2)直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]() ;
;
直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]()
故直线![]() 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
(3)显然过圆![]() 内一点的直线
内一点的直线![]() 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线![]() 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点![]() ,则
,则
![]()
直线![]() 与圆
与圆![]() 内部有交点,故
内部有交点,故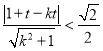
化简得,![]() ①
①
若直线![]() 与曲线C1有交点,则
与曲线C1有交点,则
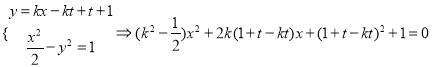
![]()
化简得,![]() ②
②
由①②得,![]()
但此时,因为![]() ,即①式不成立;
,即①式不成立;
当![]() 时,①式也不成立
时,①式也不成立
综上,直线![]() 若与圆
若与圆![]() 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点,
即圆![]() 内的点都不是“C1-C2型点” .
内的点都不是“C1-C2型点” .


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与长轴是短轴两倍的椭圆
与长轴是短轴两倍的椭圆![]() :
:![]() 相切于点
相切于点![]()
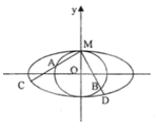
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)过点![]() 引两条互相垂直的两直线
引两条互相垂直的两直线![]() 与两曲线分别交于点
与两曲线分别交于点![]() 与点
与点![]() (均不重合).若
(均不重合).若![]() 为椭圆上任一点,记点
为椭圆上任一点,记点![]() 到两直线的距离分别为
到两直线的距离分别为![]() ,求
,求![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否为有界函数,若是,请说明理由,并写出
上是否为有界函数,若是,请说明理由,并写出![]() 的所有上界
的所有上界![]() 的集合;若不是,也请说明理由;
的集合;若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,倾斜角为a的直线经过抛物线![]() 的焦点F,且与抛物线交于A、B两点.
的焦点F,且与抛物线交于A、B两点.
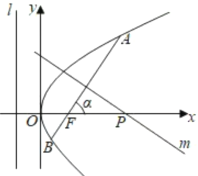
(1)求抛物线的焦点F的坐标及准线![]() 的方程;
的方程;
(2)若a为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2a为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点在x轴上,一个顶点为![]() ,离心率为
,离心率为![]() ,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
![]() 设
设![]() ,是线段
,是线段![]() 为坐标原点
为坐标原点![]() 上的一个动点,且
上的一个动点,且![]() ,求m的取值范围.
,求m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com