
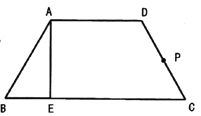
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() 为
为![]() 的中点.沿
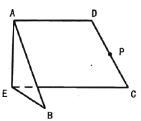
的中点.沿![]() 将梯形折成大小为
将梯形折成大小为![]() 的二面角
的二面角![]() ,若
,若![]() 内(含边界)存在一点
内(含边界)存在一点![]() ,使得
,使得![]() 平面
平面![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.
科目:高中数学 来源: 题型:
【题目】给出下列命题:
(1)若函数![]() 在
在![]() 上是减函数,则
上是减函数,则![]() ;
;
(2)直线![]() 与线段
与线段![]() 相交,其中
相交,其中![]() ,
,![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;
;
(3)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则![]() 的坐标为
的坐标为![]() ;
;
(4)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,则以
两点,则以![]() 为直径的圆恰好与直线
为直径的圆恰好与直线![]() 相切.
相切.
其中正确的命题有__________.(把所有正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l:
,直线l: ![]()

(Ⅰ)求直线l所过定点A的坐标;
(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;
(Ⅲ)已知点![]() ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点N的坐标及该常数。
为一常数,试求所有满足条件的点N的坐标及该常数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
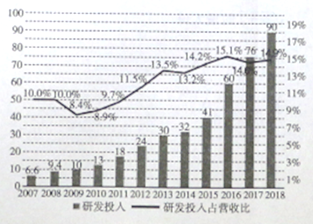
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P-ABC中,三条侧棱PA、PB、PC两两垂直,且![]() ,
,![]() ,又M是底面ABC内一点,则M到三个侧面的距离的平方和的最小值是________.
,又M是底面ABC内一点,则M到三个侧面的距离的平方和的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设λ是正实数,(1+λx)20的二项展开式为a0+a1x+a2x2+…+a20x20,其中a0,a1,…,a20 ,…,均为常数
(1)若a3=12a2,求λ的值;
(2)若a5≥an对一切n∈{0,1,…,20}均成立,求λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com