练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列是首项为1的等差数列，数列满足，且.

    （1）求数列的通项公式；

    （2）令，求数列的前项和.

    【答案】(1) ;(2) .

    【解析】试题分析: （1）根据数列的递推关系式以及等比数列的定义,得出是一个等比数列,根据基本量运算求解即可;(2)先求出等差数列的通项公式,代入,根据错位相减法求出数列的前n项和.

    试题解析:

    （1）∵，∴，∴，

    ∴是首项为，公比为3的等比数列，

    ∴，即.

    （2）由（1）知， ，∴，则，

    ∴，

    令，①

    ，②

    ①②得

    ∴.∴.

    点睛: 用错位相减法求和应注意的问题 :(1)要善于识别题目类型，特别是等比数列公比为负数的情形； (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn－qSn”的表达式； (3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为（为参数），曲线的参数方程为（为参数），以该直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）分别求曲线的极坐标方程和曲线的直角坐标方程；

    （Ⅱ）设直线交曲线于，两点，交曲线于，两点，求的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，真命题的序号是__________．

    ①“若，则”的否命题；

    ②“，函数在定义域内单调递增”的否定；

    ③“”是“”的必要条件；

    ④函数与函数的图象关于直线对称.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲盒子中有个红球，个蓝球，乙盒子中有个红球，个蓝球，同时从甲乙两个盒子中取出个球进行交换，（a）交换后，从甲盒子中取1个球是红球的概率记为.（b）交换后，乙盒子中含有红球的个数记为.则（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

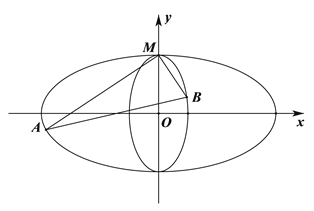
    【题目】如图，焦点在轴上的椭圆与焦点在轴上的椭圆都过点，中心都在坐标原点，且椭圆与的离心率均为．

    （Ⅰ）求椭圆与椭圆的标准方程；

    （Ⅱ）过点M的互相垂直的两直线分别与，交于点A，B（点A、B不同于点M），当的面积取最大值时，求两直线MA，MB斜率的比值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数的图象向左平移个单位长度，再向上平移1个单位长度，得到函数的图象，则函数具有性质__________．（填入所有正确性质的序号）

    ①最大值为，图象关于直线对称；

    ②图象关于轴对称；

    ③最小正周期为；

    ④图象关于点对称；

    ⑤在上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝xlnxx2﹣ax+1．

    （1）设g（x）＝f′（x），求g（x）的单调区间；

    （2）若f（x）有两个极值点x1，x2，求证：x1+x2＞2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海水养殖场使用网箱养殖的方法，收获时随机抽取了 100个网箱，测量各箱水产品的产量(单位:)，其频率分布直方图如图：

    定义箱产量在(单位:)的网箱为“稳产网箱”， 箱产量在区间之外的网箱为“非稳产网箱”.

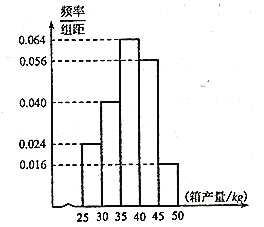
    （1）从该养殖场（该养殖场中的网箱数量是巨大的）中随机抽取3个网箱.将频率视为概率，设其中稳产网箱的个数为，求的分布列与期望；

    （2）从样本中随机抽取3个网箱，设其中稳产网箱的个数为，试比较的期望与的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．

    （1）当 时，求曲线 在点 处的切线方程；

    （2）求 的单调区间．

    查看答案和解析>>

    同步练习册答案