
ЁОЬтФПЁПФГЙЋЫОЖдЦьЯТЕФМзЁЂввСНИіУХЕъдк1жС9дТЗнЕФгЊвЕЖюЃЈЕЅЮЛЃКЭђдЊЃЉНјааЭГМЦВЂЕУЕНШчЭМелЯпЭМ.
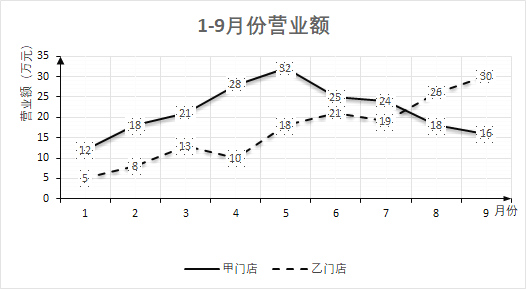
ЯТУцЙигкСНИіУХЕъгЊвЕЖюЕФЗжЮіжаЃЌДэЮѓЕФЪЧ( )
A.МзУХЕъЕФгЊвЕЖюелЯпЭМОпгаНЯКУЕФЖдГЦадЃЌЙЪЖјгЊвЕЖюЕФЦНОљжЕдМЮЊ32ЭђдЊ
B.ИљОнМзУХЕъЕФгЊвЕЖюелЯпЭМПЩжЊЃЌИУУХЕъгЊвЕЖюЕФЦНОљжЕдк[20ЃЌ25]Фк
C.ИљОнввУХЕъЕФгЊвЕЖюелЯпЭМПЩжЊЃЌЦфгЊвЕЖюзмЬхЪЧЩЯЩ§ЧїЪЦ
D.ввУХЕъдкет9ИідТЗнжаЕФгЊвЕЖюЕФМЋВюЮЊ25ЭђдЊ
ЁОД№АИЁПA
ЁОНтЮіЁП
ИљОнелЯпЭМвРДЮХаЖЯУПИібЁЯюЃКМзУХЕъЕФгЊвЕЖюЦНОљжЕдЖЕЭгк32ЭђдЊЃЌAДэЮѓЃЌЦфЫће§ШЗЃЌЕУЕНД№АИ.
ЖдгкAЃЌМзУХЕъЕФгЊвЕЖюелЯпЭМОпгаНЯКУЕФЖдГЦадЃЌгЊвЕЖюЦНОљжЕдЖЕЭгк32ЭђдЊЃЌAДэЮѓ.
ЖдгкBЃЌМзУХЕъЕФгЊвЕЖюЕФЦНОљжЕЮЊ![]() 21.6ЃЌ
21.6ЃЌ
МДИУУХЕъгЊвЕЖюЕФЦНОљжЕдкЧјМф[20ЃЌ25]ФкЃЌBе§ШЗ.
ЖдгкCЃЌИљОнввУХЕъЕФгЊвЕЖюелЯпЭМПЩжЊЃЌЦфгЊвЕЖюзмЬхЪЧЩЯЩ§ЧїЪЦЃЌCе§ШЗ.
ЖдгкDЃЌввУХЕъдкет9ИідТжаЕФгЊвЕЖюзюДѓжЕЮЊ30ЭђдЊЃЌзюаЁжЕЮЊ5ЭђдЊЃЌ
дђМЋВюЮЊ25ЭђдЊЃЌDе§ШЗ.
ЙЪбЁЃКA.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШ§РтзЖ![]() жаЃЌ
жаЃЌ![]() .
.
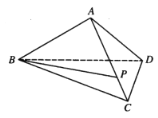
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЧЕФе§ЯвжЕ.
ЫљГЩЕФНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжгавЛХХ10ИіЮЛжУЕФПеЭЃГЕГЁЃЌМзЁЂввЁЂБћШ§СОВЛЭЌЕФГЕШЅЭЃЗХЃЌвЊЧѓУПСОГЕзѓгвСНБпЖМгаПеГЕЮЛЧвМзГЕдкввЁЂБћСНГЕжЎМфЕФЭЃЗХЗНЪНЙВга_________жж.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЦНУцABCDЃЌEЮЊPDЕФжаЕуЃЌ
ЦНУцABCDЃЌEЮЊPDЕФжаЕуЃЌ![]() .
.
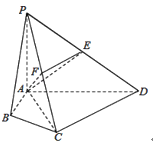
ЃЈ1ЃЉЧѓЫФРтзЖ![]() ЕФЬхЛ§VЃЛ
ЕФЬхЛ§VЃЛ
ЃЈ2ЃЉШєFЮЊPCЕФжаЕуЃЌЧѓжЄЃКЦНУц![]() ЦНУцAEFЃЛ
ЦНУцAEFЃЛ
ЃЈ3ЃЉЧѓЖўУцНЧ![]() ЕФДѓаЁ.
ЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌЁїPADЮЊЕШБпШ§НЧаЮЃЌABЃНAD![]() CDЃН2ЃЌЁЯBADЃНЁЯADCЃН90ЁуЃЌЁЯPDCЃН60ЁуЃЌEЮЊBCЕФжаЕу.
CDЃН2ЃЌЁЯBADЃНЁЯADCЃН90ЁуЃЌЁЯPDCЃН60ЁуЃЌEЮЊBCЕФжаЕу.
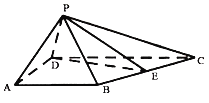
ЃЈ1ЃЉжЄУїЃКADЁЭPE.
ЃЈ2ЃЉЧѓжБЯпPAгыЦНУцPDEЫљГЩНЧЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ0ЃМmЃМ2,ЖЏЕуMЕНСНЖЈЕуF1ЃЈЉm,0ЃЉ,F2ЃЈm,0ЃЉЕФОрРыжЎКЭЮЊ4,ЩшЕуMЕФЙьМЃЮЊЧњЯпC,ШєЧњЯпCЙ§Еу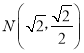 .
.
ЃЈ1ЃЉЧѓmЕФжЕвдМАЧњЯпCЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§ЖЈЕу![]() ЧваБТЪВЛЮЊСуЕФжБЯпlгыЧњЯпCНЛгкA,BСНЕу.жЄУїЃКвдABЮЊжБОЖЕФдВЙ§ЧњЯпCЕФгвЖЅЕу.
ЧваБТЪВЛЮЊСуЕФжБЯпlгыЧњЯпCНЛгкA,BСНЕу.жЄУїЃКвдABЮЊжБОЖЕФдВЙ§ЧњЯпCЕФгвЖЅЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋ6ИіЪ§2ЁЂ0ЁЂ1ЁЂ9ЁЂ20ЁЂ19АДШЮвтДЮађХХГЩвЛааЃЌЦДГЩвЛИі8ЮЛЪ§(ЪзЮЛВЛЮЊ0)ЃЌдђВњЩњЕФВЛЭЌЕФ8ЮЛЪ§ЕФИіЪ§ЮЊ______ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФРтзЖ![]() ЕФЕзУцABCDЪЧБпГЄЮЊaЕФСтаЮЃЌ
ЕФЕзУцABCDЪЧБпГЄЮЊaЕФСтаЮЃЌ![]() УцABCDЃЌ
УцABCDЃЌ![]() ЃЌEЃЌFЗжБ№ЪЧCDЃЌPCЕФжаЕу.
ЃЌEЃЌFЗжБ№ЪЧCDЃЌPCЕФжаЕу.

ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУцPABЃЛ
ЦНУцPABЃЛ
ЃЈ2ЃЉMЪЧPBЩЯЕФЖЏЕуЃЌEMгыЦНУцPABЫљГЩЕФзюДѓНЧЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
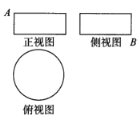
ЁОЬтФПЁПФГдВжљЕФИпЮЊ2ЃЌЕзУцжмГЄЮЊ16ЃЌдђЦфЬхЛ§ЮЊ_________ЃЌШєИУдВжљЕФШ§ЪгЭМШчЭМЫљЪОЃЌдВжљБэУцЩЯЕФЕуMдке§ЪгЭМЩЯЕФЖдгІЕуЮЊAЃЌдВжљБэУцЩЯЕФЕуNдкВрЪгЭМЩЯЕФЖдгІЕуЮЊBЃЌдђдкДЫдВжљВрУцЩЯЃЌДгMЕНNЕФТЗОЖжаЃЌзюЖЬТЗОЖЕФГЄЖШЮЊ___________.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com