
如果对定义在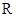 上的函数
上的函数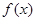 ,对任意两个不相等的实数
,对任意两个不相等的实数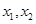 ,都有
,都有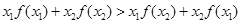 ,则称函数
,则称函数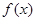 为“
为“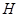 函数”.给出下列函数①
函数”.给出下列函数①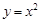 ;②
;②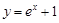 ;③
;③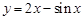 ;④
;④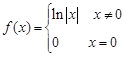 .以上函数是“
.以上函数是“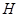 函数”的所有序号为 .
函数”的所有序号为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
下图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数 对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与
轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与 轴交于点N(
轴交于点N( ),则
),则 的象就是
的象就是 ,记作
,记作

给出下列命题:① ; ②
; ② ; ③
; ③ 是奇函数; ④
是奇函数; ④ 在定义域上单调递增,则所有真命题的序号是______________.(填出所有真命题的序号)
在定义域上单调递增,则所有真命题的序号是______________.(填出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出定义:若 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数 最近的整数,记作
最近的整数,记作 ,即
,即 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题:
① 的定义域是
的定义域是 ,值域是
,值域是 ;
;
②点 是
是 的图像的对称中心,其中
的图像的对称中心,其中 ;
;
③函数 的最小正周期为
的最小正周期为 ;
;
④函数 在
在 上是增函数.
上是增函数.
则上述命题中真命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com