
【题目】已知圆锥曲线![]() 的两个焦点坐标是
的两个焦点坐标是![]() ,且离心率为
,且离心率为![]() ;
;
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 表示曲线
表示曲线![]() 的
的![]() 轴左边部分,若直线
轴左边部分,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的取值范围;
的取值范围;
(3)在条件(2)下,如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据离心率可得曲线为双曲线,然后根据焦点及离心率可得![]() ,进而得到曲线方程.(2)将直线方程代入双曲线方程得到二次方程
,进而得到曲线方程.(2)将直线方程代入双曲线方程得到二次方程![]() ,根据题意可得该二次方程有两个负数根,结合根与系数的关系可得所求.(3)由弦长公式及(2)中实数
,根据题意可得该二次方程有两个负数根,结合根与系数的关系可得所求.(3)由弦长公式及(2)中实数![]() 的取值范围可得
的取值范围可得![]() ,于是可得直线AB的方程.设C(x0,y0),由条件
,于是可得直线AB的方程.设C(x0,y0),由条件![]() 可得
可得![]() ,再根据点
,再根据点![]() 在双曲线上可求得
在双曲线上可求得![]() .
.
(1)由e=![]() 知,曲线E是以F1(﹣
知,曲线E是以F1(﹣![]() ,0),F2(
,0),F2(![]() ,0)为焦点的双曲线,
,0)为焦点的双曲线,
且c=![]() ,
,![]() ,
,
解得![]() ,
,
∴b2=2﹣1=1,
故双曲线E的方程是x2﹣y2=1.
(2)由![]() 消去
消去![]() 整理得
整理得![]()
设A(x1,y1),B(x2,y2),
由题意可得方程有两个负数根,
∴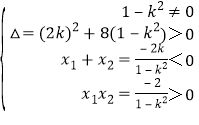 ,解得
,解得![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由题意及(2)得
6![]() =|
=|![]() |=
|=![]() |x1﹣x2|=
|x1﹣x2|=![]()
![]() =
=![]() ,
,
整理得28k4﹣55k2+25=0,
解得![]() 或
或![]() ,
,
又﹣![]() ,
,
∴k=﹣![]() ,
,
故直线AB的方程为![]() .
.
设C(x0,y0),由![]() =m
=m![]() ,得(x1,y1)+(x2,y2)=(mx0,my0),
,得(x1,y1)+(x2,y2)=(mx0,my0),
又![]() =﹣4
=﹣4![]() ,y1+y2=k(x1+x2)﹣2=8,
,y1+y2=k(x1+x2)﹣2=8,
∴![]() .
.
∵点![]() 在曲线E上,
在曲线E上,
∴![]() ,解得m=±4,
,解得m=±4,
当m=﹣4时,所得的点在双曲线的右支上,不合题意,
∴m=4为所求.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(2cos2 ![]() +sinx)+b
+sinx)+b
(1)若a=﹣1,求f(x)的单调增区间;
(2)若x∈[0,π]时,f(x)的值域是[5,8],求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
(Ⅰ)求n的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,O为AD中点.
,O为AD中点.

(1)求证:PO⊥平面ABCD;
(2)求直线BD与平面PAB所成角的正弦值;
(3)线段AD上是否存在点![]() ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B. “![]() 且
且![]() 为真命题”是“
为真命题”是“![]() 或
或![]() 为真命题” 的必要不充分条件
为真命题” 的必要不充分条件
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命题![]() :“
:“![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{ ![]() }中,已知
}中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
将数列的等式关系两边取倒数![]() 是公差为
是公差为![]() 的等差数列,再根据等差数列求和公式得到数列通项
的等差数列,再根据等差数列求和公式得到数列通项![]() ,再取倒数即可得到数列{
,再取倒数即可得到数列{![]() }的通项.
}的通项.
将等式![]() 两边取倒数得到
两边取倒数得到![]() ,
,![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() =
=![]() ,根据等差数列的通项公式的求法得到
,根据等差数列的通项公式的求法得到![]() ,故
,故![]() =
=![]() .
.
故答案为:B.
【点睛】
这个题目考查的是数列通项公式的求法,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;还有构造新数列的方法,取倒数,取对数的方法等等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;还有构造新数列的方法,取倒数,取对数的方法等等.
【题型】单选题
【结束】
9
【题目】在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是 ( )

(A) [15,20](B) [12,25] (C) [10,30](D) [20,30]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把函数y=sin(2x+
)的图象,只需把函数y=sin(2x+ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos(ωx﹣φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ).则下列说法错误的是( )
).则下列说法错误的是( ) 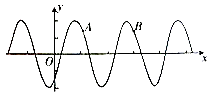
A.φ= ![]()
B.函数f(x)的一条对称轴为x= ![]()
C.为了得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移 ![]() 个单位
个单位
D.函数f(x)的一个单调减区间为[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com