
����Ŀ�������������������չ��ͬʱҲ����شٽ��˿����ҵ�ķ�չ��Ϊ�˸��õط���ͻ���ij��ݹ�˾ʹ�ÿͻ�����ϵͳ�Կ�ݷ�����Ա�ķ���������ۣ�ÿ�¸��ݿͻ�������ѡ�������֮��������֪�����С����С����ÿ���±���ѡΪ�����֮�����ĸ��ʶ���![]() ����С���ڵ�һ���ȵ�3��������2���¶�����Ϊ�����֮�����ĸ���Ϊ_______����С�����ϰ����6�����б���Ϊ�����֮�����Ĵ���Ϊ�������X�����������X�ķ���
����С���ڵ�һ���ȵ�3��������2���¶�����Ϊ�����֮�����ĸ���Ϊ_______����С�����ϰ����6�����б���Ϊ�����֮�����Ĵ���Ϊ�������X�����������X�ķ���![]() ______��
______��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĵ㣬
�ϵĵ㣬![]() ����
����![]() ����ͼ�٣�.���ı���
����ͼ�٣�.���ı���![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() ����ͼ�ڣ�.������Ĺ����У������б�����
����ͼ�ڣ�.������Ĺ����У������б�����

��![]() ƽ��
ƽ��![]() ��
��
���ĵ�![]() ��
��![]() ��
��![]() ��
��![]() ���ܹ��棻
���ܹ��棻
����![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ��
��
��ƽ��![]() ��ƽ��
��ƽ��![]() ���ܴ�ֱ.������ȷ����__________.
���ܴ�ֱ.������ȷ����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)![]() sin(��x+��)��cos(��x+��)(0<��<��,��>0)Ϊż��������y=f(x)ͼ��������ڶԳ����ľ���Ϊ
sin(��x+��)��cos(��x+��)(0<��<��,��>0)Ϊż��������y=f(x)ͼ��������ڶԳ����ľ���Ϊ![]() ����f(
����f(![]() )��ֵΪ�� ��
)��ֵΪ�� ��
A.��1B.1C.![]() .D.
.D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊʵ������
Ϊʵ������![]() ����
����
����![]() ʱ��
ʱ��
����![]() ���жϺ���
���жϺ���![]() ����ż�ԣ���˵�����ɣ�
����ż�ԣ���˵�����ɣ�
����֤������![]() ��
��![]() ������������
������������
�����輯��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ����
��ȡֵ��Χ����![]() ��ʾ����
��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����״������һ�����Ͳ������壬��֪�������ð�Լ��ж������ۺ���![]() �����ؼ��Ժ����ۺ���
�����ؼ��Ժ����ۺ���![]() �Ƚ����ؼ���������������ֲ���ȫ�����ӵ�����״����
�Ƚ����ؼ���������������ֲ���ȫ�����ӵ�����״����![]() ����ǰ��δ�������з��ֵĹ�״�����¶��꣮�˸�Ⱦ������״�����������к�����֢״�����ȡ����ԡ����ٺͺ������ѵȣ��ڽ����ز����и�Ⱦ�ɵ��·��ס����ؼ��Ժ����ۺ�������˥�ߣ�����������
����ǰ��δ�������з��ֵĹ�״�����¶��꣮�˸�Ⱦ������״�����������к�����֢״�����ȡ����ԡ����ٺͺ������ѵȣ��ڽ����ز����и�Ⱦ�ɵ��·��ס����ؼ��Ժ����ۺ�������˥�ߣ�����������
ijҩ���о���Ϊɸ����ֲ�������Ҫ����ѪҺ�Ƿ�Ϊ���ԣ�����![]() ��
��![]() ����
����![]() ����ѪҺ������ÿ������ȡ���Ŀ�������ȣ����������ּ��鷽ʽ��
����ѪҺ������ÿ������ȡ���Ŀ�������ȣ����������ּ��鷽ʽ��
��ʽһ����ݼ�������Ҫ����![]() �Σ�
�Σ�
��ʽ������ϼ��飬��![]() ��ѪҺ�����ֱ�ȡ�������һ����飬��������Ϊ���ԣ�����
��ѪҺ�����ֱ�ȡ�������һ����飬��������Ϊ���ԣ�����![]() �ݵ�ѪҺȫΪ���ԣ������
�ݵ�ѪҺȫΪ���ԣ������![]() ��ѪҺ����ֻҪ����һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��
��ѪҺ����ֻҪ����һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��![]() ��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����
��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����![]() ������ݼ��飬��ʱ��
������ݼ��飬��ʱ��![]() ��ѪҺ�ļ�������ܹ�Ϊ
��ѪҺ�ļ�������ܹ�Ϊ![]() �Σ������ڽ��ܼ����ѪҺ�����У�ÿ�������ļ����������Ի������Զ��Ƕ����ģ���ÿ�����������Խ���ĸ���Ϊ
�Σ������ڽ��ܼ����ѪҺ�����У�ÿ�������ļ����������Ի������Զ��Ƕ����ģ���ÿ�����������Խ���ĸ���Ϊ![]() ��
��
��1��������6��ѪҺ����������ֻ��2������Ϊ���ԣ�������ȡ3����������ҽѧ�о�����������1��Ϊ���������ĸ��ʣ�
��2�����轫![]() ��
��![]() ��
��![]() ����ѪҺ�������м��飬�Dz�����ݼ��鷽ʽ��������Ҫ������ܴ���Ϊ
����ѪҺ�������м��飬�Dz�����ݼ��鷽ʽ��������Ҫ������ܴ���Ϊ![]() �����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ
�����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ![]() ��
��
�����ø���ͳ�Ƶ�֪ʶ����![]() ������
������![]() ����
����![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ![]() ��
��
����![]() ������ؼ���
������ؼ���![]() ��أ���������
��أ���������![]() ����
����![]() ����
����![]() ʱ�������۲��ú��ּ��鷽ʽ���ã�
ʱ�������۲��ú��ּ��鷽ʽ���ã�
�ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У��ı���ABCD�Ǿ��Σ�ƽ��
�У��ı���ABCD�Ǿ��Σ�ƽ��![]() ƽ��ABCD��
ƽ��ABCD��![]() ��E��SB���е㣬M��CD������һ�㣮
��E��SB���е㣬M��CD������һ�㣮
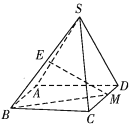
��1����֤��![]() ��
��
��2����![]() ��
��![]() ��
��![]() ƽ��SAD����ֱ��BM��ƽ��SAB���ɽǵ�����ֵ��
ƽ��SAD����ֱ��BM��ƽ��SAB���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��������
��������![]() ��
��![]() ��ǰ
��ǰ![]() ��ͷֱ�Ϊ
��ͷֱ�Ϊ![]() ��
��![]() .
.
��1��������![]() �ǵȲ����У���
�ǵȲ����У���![]() ��
��![]() ��
��
��2��������![]() �ǹ���Ϊ2�ĵȱ�����.
�ǹ���Ϊ2�ĵȱ�����.
����![]() ��
��
���Ƿ����ʵ��![]() ��ʹ
��ʹ![]() ��������Ȼ��
��������Ȼ��![]() �������������ڣ���
�������������ڣ���![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ���
�����ҽ���ֱ���![]() ��
��![]() ����
����![]() ����Բ
����Բ![]() �ϳ�����˵������һ�㣬����
�ϳ�����˵������һ�㣬����![]() ��
��![]() ����
����![]() ���ڽ�ƽ����
���ڽ�ƽ����![]() ��
��![]() �ij����ڵ�
�ij����ڵ�![]() ��
��
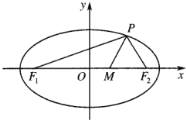
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������SһABC�У���ABC���SBC���DZ߳�Ϊ1���������Σ������A��BC��S�Ĵ�СΪ![]() ����S��A��B��C�ĵ㶼����O�ı����ϣ�����O�ı����Ϊ�� ��
����S��A��B��C�ĵ㶼����O�ı����ϣ�����O�ı����Ϊ�� ��
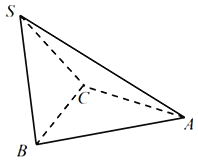
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.3��
��D.3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com