
分析 (1)利用向量的数量积运算、二倍角公式,两角和的正弦公式化简解析式,由正弦函数的增区间求出f(x)单调递增区间;
(2)由三角函数图象的平移法则求出g(x),由由x的范围和正弦函数的性质求出g(x)的值域,由条件和恒成立问题转化为求最值,从而求出实数k的取值范围.
解答 解:(1)由题意得,f(x)=$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{3}$sin$\frac{x}{4}$cos$\frac{x}{4}$+cos2$\frac{x}{4}$
=$\frac{\sqrt{3}}{2}$sin$\frac{x}{2}$+$\frac{1}{2}$cos$\frac{x}{2}$+$\frac{1}{2}$=$sin(\frac{x}{2}+\frac{π}{6})+\frac{1}{2}$,
由$2kπ-\frac{π}{2}≤\frac{x}{2}+\frac{π}{6}≤2kπ+\frac{π}{2}(k∈Z)$得,
$4kπ-\frac{4π}{3}≤x≤4kπ+\frac{2π}{3}(k∈Z)$,
∴函数f(x)的单调递增区间是$[4kπ-\frac{4π}{3},4kπ+\frac{2π}{3}](k∈Z)$;
(2)将f(x)的图象向右平移$\frac{2π}{3}$个单位长度得到g(x)=$sin(\frac{x}{2}-\frac{π}{6})+\frac{1}{2}$的图象,
当$x∈[0,\frac{7π}{3}]$时,$-\frac{π}{6}≤\frac{x}{2}-\frac{π}{6}≤π$,∴$-\frac{1}{2}≤sin(\frac{x}{2}-\frac{π}{6})≤1$,
∴$0≤sin(\frac{x}{2}-\frac{π}{6})+\frac{1}{2}≤\frac{3}{2}$,
∵g(x)-k≤0在区间[0,$\frac{7π}{3}$]上恒成立,
∴k≥g(x)max=$\frac{3}{2}$,
∴实数k的取值范围是[$\frac{3}{2}$,+∞).
点评 本题考查正弦函数的图象与性质,向量的数量积运算、二倍角公式,两角和的正弦公式等,以及恒成立问题的转化,考查转化思想,数形结合思想,化简、变形能力.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
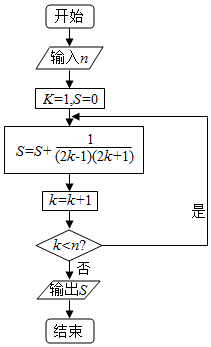
| A. | $\frac{2016}{4033}$ | B. | $\frac{2017}{4035}$ | C. | $\frac{4032}{4033}$ | D. | $\frac{4034}{4035}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤3} | B. | {x|x≥3或x≤-1} | C. | {x|-3≤x≤1} | D. | {x|x≤-3或x≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 4 | 2 | 2 | 1 |
| A. | $\stackrel{∧}{y}$=-x+2.8 | B. | $\stackrel{∧}{y}$=-x+3 | C. | $\stackrel{∧}{y}$=-1.2x+2.6 | D. | $\stackrel{∧}{y}$=2x+2.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com