
【题目】已知函数f(x)=![]() (a<0).
(a<0).
(1)当a=-1时,求函数f(x)的极值;
(2)若函数F(x)=f(x)+1没有零点,求实数a的取值范围.
【答案】(1)极小值为f(2)=-![]() ,无极大值.(2) (-e2,0).
,无极大值.(2) (-e2,0).
【解析】试题分析:(1)将参数值代入得到表达式,根据极值的定义得到函数f(x)的极小值为f(2)=-![]() ;(2)研究函数的F(x)=f(x)+1单调性,画出函数的大概变化趋势,使得函数和x轴没有交点即可。
;(2)研究函数的F(x)=f(x)+1单调性,画出函数的大概变化趋势,使得函数和x轴没有交点即可。
解析:
(1)当a=-1时,f(x)=![]() ,f′(x)=
,f′(x)=![]() .
.
由f′(x)=0,得x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (-∞,2) | 2 | (2,+∞) |
f′(x) | - | 0 | + |
f(x) | ? | 极小值 | ? |
所以,函数f(x)的极小值为f(2)=-![]() ,函数f(x)无极大值.
,函数f(x)无极大值.
(2)F′(x)=f′(x)=![]() =
=![]() .
.
当a<0时,F′(x),F(x)随x的变化情况如下表:
x | (-∞,2) | 2 | (2,+∞) |
F′(x) | - | 0 | + |
F(x) | ? | 极小值 | ? |
若使函数F(x)没有零点,当且仅当F(2)=![]() +1>0,
+1>0,
解得a>-e2,所以此时-e2<a<0.
故实数a的取值范围为(-e2,0).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
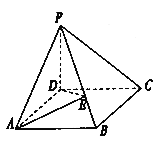
【题目】如图在棱锥![]() 中,
中, ![]() 为矩形,
为矩形, ![]() 面
面![]() ,
, ![]() ,
, ![]() 与面
与面![]() 成
成![]() 角,
角, ![]() 与面
与面![]() 成
成![]() 角.
角.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 面
面![]() ,若存在确定
,若存在确定![]() 点位置,若不存在,请说明理由;
点位置,若不存在,请说明理由;
(2)当![]() 为
为![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB ∥EF,矩形ABCD所在平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
(1)求证:平面DAF⊥平面CBF;
(2)求直线AB与平面CBF所成角的大小;
(3)求AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax,g(x)=lnx,h(x)=f(x)+g(x).
(1)若函数y=h(x)的单调减区间是![]() ,求实数a的值;
,求实数a的值;
(2)若f(x)≥g(x)对于定义域内的任意x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.

(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P B1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com