Question

9．如图在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=$\sqrt{3}$，BD=CD=1，另一个侧面是正三角形
（1）求证：AD⊥BC；
（2）求二面角B-AC-D的余弦值；
（3）点E在直线AC上，当直线ED与平面BCD成30°角若时，求点C到平面BDE的距离．

Answer 1

分析 （1）取BC中点O，连结AO、DO，则AO⊥BC，DO⊥BC，由此能证明BC⊥AD．
（2）作BM⊥AC于M，作MN⊥AC，交AD于N，则∠BMN就是二面角B-AC-D的平面角，由此利用余弦定理能求出二面角B-AC-D的余弦值．
（3）过A作AH⊥平面BCD，交DO延长线于H，连结CH，设E是所求的点，过E作EF⊥CH于F，连结FD，∠EDF就是直线ED与平面BCD所成角，由V_E-BCD=V_C-BED，能求出点C到平面BDE的距离．

解答 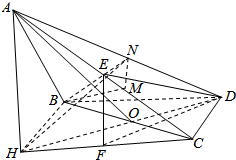证明：（1）取BC中点O，连结AO、DO，
∵在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，
且AD=$\sqrt{3}$，BD=CD=1，另一个侧面是正三角形，
∴AO⊥BC，DO⊥BC，∴BC⊥面AOD，
∴BC⊥AD．
解：（2）作BM⊥AC于M，作MN⊥AC，交AD于N，
则∠BMN就是二面角B-AC-D的平面角，
∵AB=AC=BC=$\sqrt{2}$，M是AC中点，
∴BM=$\frac{\sqrt{6}}{2}$，MN=$\frac{1}{2}CD=\frac{1}{2}$，BN=$\frac{1}{2}AD=\frac{\sqrt{3}}{2}$，
由余弦定理得cos∠BMN=$\frac{\frac{3}{2}+\frac{1}{4}-\frac{3}{4}}{2×\frac{\sqrt{6}}{2}×\frac{1}{2}}$=$\frac{\sqrt{6}}{3}$，
∴二面角B-AC-D的余弦值为$\frac{\sqrt{6}}{3}$．
（3）过A作AH⊥平面BCD，交DO延长线于H，连结CH，
设E是所求的点，过E作EF⊥CH于F，连结FD，
则EF∥AH，
∴EF⊥面BCD，∠EDF就是直线ED与平面BCD所成角，∴∠EDF=30°，
设EF=x，由题意AH=CH=1，CF=x，FD=$\sqrt{1+{x}^{2}}$，
∴tan∠EDF=$\frac{x}{\sqrt{1+{x}^{2}}}$=$\frac{\sqrt{3}}{3}$，解得x=$\frac{\sqrt{2}}{2}$，
则CE=1，设点C到平面BDE的距离为d，
∵V_E-BCD=V_C-BED，
∴$\frac{1}{3}×\frac{1}{2}×1×1×\frac{\sqrt{2}}{2}$=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{6}}{2}×d$，
解得d=$\frac{\sqrt{3}}{3}$，∴点C到平面BDE的距离为$\frac{\sqrt{3}}{3}$．

点评 本题考查异面直线垂直的证明，考查二面角的余弦值的求法，考查点到平面的距离的求法，是中档题，解题时要认真审题，注意余弦定理、等体积法的合理运用．