
|
| π |
| 2 |
| 3π |
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
|
| ||
| 2 |
| π |
| 2 |
|
| 3π |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| 1 |
| 2 |
| 3 |
| d |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| m |
| 3 |
| n |
| m |
| n |
| 1 |
| 2 |
| 3 |
| d |
| e |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省宜春市上高二中高二(上)第三次月考数学试卷(文科)(解析版) 题型:解答题
 sinx,cosx),
sinx,cosx), =(cosx,-cosx),x∈R,定义函数f(x)=
=(cosx,-cosx),x∈R,定义函数f(x)=
 ,f(C)=0,若向量
,f(C)=0,若向量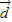 =(1,sinA)与
=(1,sinA)与  =(2,sinB)共线,求边a,b的值及△ABC的面积S?
=(2,sinB)共线,求边a,b的值及△ABC的面积S?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com