
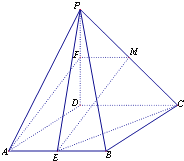
【题目】如图,在四棱锥PABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点。

(1)求直线AF与EC所成角的正弦值;
(2)求PE与平面PDB所成角的正弦值。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 作FM∥CD交PC于M,得出AF∥EM,∠MEC为直线AF与EC所成角或其补角,在直角三角形中即可得解.
(2) 运用直线平面所成角的定义得出夹角,转化为直角三角形中求解即可.
(1)作FM∥CD交PC于M.
∵点F为PD中点,∴FM=![]() CD.
CD.
∴AE=![]() AB=FM,
AB=FM,
∴AEMF为平行四边形,∴AF∥EM,
∠MEC为直线AF与EC所成角或其补角。
EM=AF=![]() ,MC=
,MC=![]() ,EC=
,EC=![]() ,∴ΔMEC为RtΔMEC
,∴ΔMEC为RtΔMEC
sin∠MEC=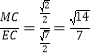
(2)连接AC,BD交于O,连接EG
∵点E,O分别为AB和AC中点。
∴AO∥EG,
∵AC⊥平面PBD,
∴EG⊥平面PBD,
根据直线与平面所成角的定义可得:∠EPG为PE与平面PDB所成角,
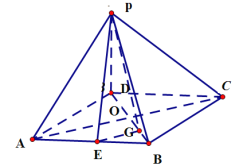
Rt△EGP中,AO=![]() ,EG=
,EG=![]() ,
,
DE=![]() ,PE=
,PE=![]() ,
,
∴sin∠EPG=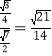


科目:高中数学 来源: 题型:
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)(ⅰ)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ⅱ)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M是正四面体ABCD棱AB的中点,N是棱CD上异于端点C,D的任一点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)若N为中点,则MN与AD所成角为60°;
(3)平面CDM⊥平面ABN;
(4)不存在点N,使得过MN的平面与AC垂直.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知抛物线C:y2=4x的焦点为F,直线l经过点F且与抛物线C相交于A、B两点.

(1)若线段AB的中点在直线y=2上,求直线l的方程;
(2)若线段|AB|=20,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球,乙罐中有
个黑球,乙罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球。先从甲罐中随机取出一球放入乙罐,分别以
个黑球。先从甲罐中随机取出一球放入乙罐,分别以![]() 和
和![]() 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以![]() 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
①![]() ; ② 事件
; ② 事件![]() 与事件
与事件![]() 相互独立;③
相互独立;③![]()
④![]() 是两两互斥的事件;
是两两互斥的事件;
⑤![]() 的值不能确定,因为它与
的值不能确定,因为它与![]() 中哪一个发生有关
中哪一个发生有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为4米,水轮圆心![]() 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点
距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点![]() 从水中浮现(图中点
从水中浮现(图中点![]() )开始计算时间.
)开始计算时间.
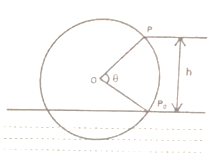
(1)将点![]() 距离水面的高度
距离水面的高度![]() (米)表示为时间
(米)表示为时间![]() (秒)的函数;
(秒)的函数;
(2)在水轮旋转一圈内,有多长时间点![]() 离开水面?
离开水面?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
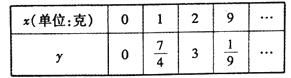
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com